
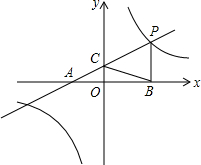
 如图,点P是直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$在第一象限内的一个交点,直线y=$\frac{1}{2}$x+2与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9,则△PBC的面积为( )
如图,点P是直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$在第一象限内的一个交点,直线y=$\frac{1}{2}$x+2与x轴、y轴的交点分别为A、C,过P作PB垂直于x轴,若AB+PB=9,则△PBC的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
分析 由直线y=$\frac{1}{2}$x+2与x轴、y轴的交点分别为A、C,确定出A、C的坐标,根据PB∥OC求得PB的长,进而求得OB的长,然后根据三角形的面积公式求得即可.
解答 解:由直线y=$\frac{1}{2}$x+2与x轴、y轴的交点分别为A、C,
∴A(-4,00,C(0,2),
∴OA=4,OC=2,
∵PB⊥x轴,
∴PB∥OC,
∴$\frac{OA}{AB}$=$\frac{OC}{PB}$,即$\frac{4}{9-PB}$=$\frac{2}{PB}$,
∴PB=3,
∴AB=6,
OB=2,
∴△PBC的面积=$\frac{1}{2}$PB•OB=$\frac{1}{2}×3×2$=3,
故选C.
点评 此题考查了反比例函数与一次函数的交点,利用了数形结合的思想,数形结合思想是数学中重要的思想方法.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
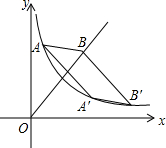 如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,设点B的横坐标为m,试用m的式子表示出点B′的坐标,并求出m的值.
如图,已知反比例函数y=$\frac{k}{x}$(x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,设点B的横坐标为m,试用m的式子表示出点B′的坐标,并求出m的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
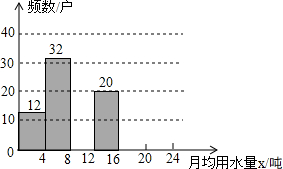 2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.| 月均用水量x(吨) | 频数(户) | 频率 |
| 0<x≤4 | 12 | a |
| 4<x≤8 | 32 | 0.32 |
| 8<x≤12 | b | c |
| 12<x≤16 | 20 | 0.2 |
| 16<x≤20 | 8 | 0.08 |
| 20<x≤24 | 4 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com