
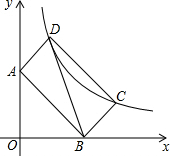
 如图,在平面直角坐标系中,矩形ABCD的边AB所在直线的解析式为y=kx+2,顶点C、D在反比例函数y=$\frac{m}{x}$(m>0)的图象上,若tan∠ADB=2.则点D的坐标为(1,3).
如图,在平面直角坐标系中,矩形ABCD的边AB所在直线的解析式为y=kx+2,顶点C、D在反比例函数y=$\frac{m}{x}$(m>0)的图象上,若tan∠ADB=2.则点D的坐标为(1,3). 分析 过点D作DE⊥y轴于E,过点C作CF⊥x轴,根据直线的解析式求出点A、B的坐标,从而得到OA、OB.易证△AED∽△BOA,根据相似三角形的性质可求出ED、AE,从而可得到点D的坐标(用k表示),同理可得到点C的坐标(用k表示),然后根据点D、C在反比例函数的图象上得到关于k的方程,就可解决问题.
解答 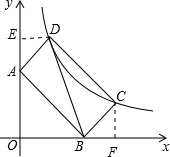 解:过点D作DE⊥y轴于E,过点C作CF⊥x轴,如图所示.
解:过点D作DE⊥y轴于E,过点C作CF⊥x轴,如图所示.
∵点A、B是直线y=kx+2分别与y轴、x轴的交点,
∴A(0,2),B(-$\frac{2}{k}$,0),
∴OA=2,OB=-$\frac{2}{k}$.
∵四边形ABCD是矩形,
∴∠A=90°,AD=BC.
∵tan∠ADB=2,
∴$\frac{AB}{AD}$=2,$\frac{AB}{BC}$=2.
∵∠DEA=∠AOB=90°,∠EAD=∠ABO=90°-∠OAB,
∴△AED∽△BOA,
∴$\frac{ED}{OA}$=$\frac{AE}{OB}$=$\frac{AD}{AB}$=$\frac{1}{2}$,
∴ED=1,AE=-$\frac{1}{k}$,
∴点D(1,2-$\frac{1}{k}$).
同理:点C(1-$\frac{2}{k}$,-$\frac{1}{k}$).
∵点C、D都在反比例函数y=$\frac{m}{x}$(m>0)的图象上,
∴1×(2-$\frac{1}{k}$)=(1-$\frac{2}{k}$)•(-$\frac{1}{k}$),
∴k=±1.
∵k<0,
∴k=-1,
∴点D的坐标为(1,3).
点评 本题主要考查了直线与反比例函数图象上点的坐标特征、矩形的性质、相似三角形的性质、三角函数的定义等知识,构造K型相似得到点D、C的坐标是解决本题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
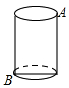 如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$.
如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若甲对,则乙对 | B. | 若甲错,则乙对 | C. | 若乙对,则甲对 | D. | 若乙错,则甲错 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
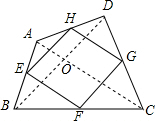 已知点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,若四边形EFGH为正方形,则原四边形ABCD应具备什么条件?说明你判断的理由.
已知点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,若四边形EFGH为正方形,则原四边形ABCD应具备什么条件?说明你判断的理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
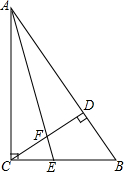 如图,在△ABC中,∠ACB=90°,∠CAB=30°,AE是△ABC的角平分线,CD是高,AE与CD相交于F点.若BE=4,则DF的长是( )
如图,在△ABC中,∠ACB=90°,∠CAB=30°,AE是△ABC的角平分线,CD是高,AE与CD相交于F点.若BE=4,则DF的长是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com