
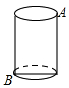
 如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$.
如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 要为一幅长30cm、宽24cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的$\frac{19}{80}$,镜框边的宽度应是多少厘米?
要为一幅长30cm、宽24cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的$\frac{19}{80}$,镜框边的宽度应是多少厘米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
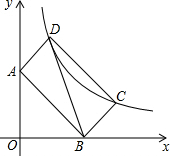 如图,在平面直角坐标系中,矩形ABCD的边AB所在直线的解析式为y=kx+2,顶点C、D在反比例函数y=$\frac{m}{x}$(m>0)的图象上,若tan∠ADB=2.则点D的坐标为(1,3).
如图,在平面直角坐标系中,矩形ABCD的边AB所在直线的解析式为y=kx+2,顶点C、D在反比例函数y=$\frac{m}{x}$(m>0)的图象上,若tan∠ADB=2.则点D的坐标为(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com