
分析 根据标准差的意义可得答案.标准差反映数据的波动大小,即数据离散程度.
解答 解:由于标准差反映数据的波动情况,所以能够刻画一组数据离散程度的统计量是标准差,
1,0,-1,-2,-3的平均数是$\frac{1+0-1-2-3}{5}=-1$,
这组数据的方差为$\frac{1}{5}×[(1+1)^{2}+(0+1)^{2}+(-1+1)^{2}+(-2+1)^{2}+(-3+1)^{2}]$=2,
所以标准差是$\sqrt{2}$.
与上述数据离散程度相同的数据为2,1,0,-1,-2;
故答案为:$\sqrt{2}$;2,1,0,-1,-2
点评 此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.反映数据集中程度的统计量有平均数、中位数、众数方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:填空题
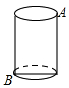 如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$.
如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
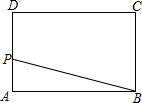 如图,P是矩形ABCD的边上的动点,当P从A点出发沿A→D→C→B运动到达B点时,△APB的面积s与运动时间t的函数关系的图象大致是( )
如图,P是矩形ABCD的边上的动点,当P从A点出发沿A→D→C→B运动到达B点时,△APB的面积s与运动时间t的函数关系的图象大致是( )| A. | 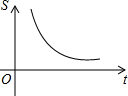 | B. | 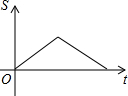 | C. |  | D. | 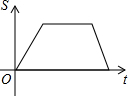 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2{a^2}}$ | D. | $\sqrt{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com