
分析 分两种情况:DE<BC、DE>BC,先根据正方形的性质证明△FDE∽△FBC可得AF=CF,由AF=2CE可得$\frac{CE}{CF}$即$\frac{FE}{FC}$,由△FDE∽△FBC可得$\frac{DE}{BC}=\frac{FE}{FC}$,继而可得tan∠DCE的值.
解答 解:①如图1,当DE<BC时,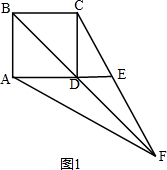
∵四边形ABCD是正方形,
∴∠ADB=∠CDB=45°,AD=CD=BC,AD∥BC,
∴∠ADF=∠CDF=135°,
在△ADF和△CDF中,
∵$\left\{\begin{array}{l}{AD=CD}\\{∠ADF=∠CDF}\\{DF=DF}\end{array}\right.$,
∴△ADF≌△CDF(SAS),
∴AF=CF,又∵AF=2CE,
∴CE=$\frac{1}{2}$CF,
∴EF=$\frac{1}{2}$CF,
∵AD∥BC,
∴△FDE∽△FBC,
∴$\frac{FE}{FC}=\frac{DE}{BC}=\frac{1}{2}$,
∵BC=CD,
∴$\frac{DE}{CD}=\frac{1}{2}$,
∴在RT△DCE中,tan∠DCE=$\frac{DE}{CD}=\frac{1}{2}$;
②如图2,当DE>BC时,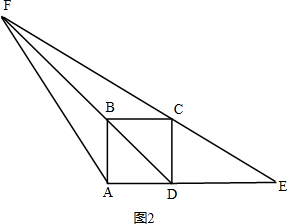
与(1)同理可得AF=CF=2CE,
∴EF=3CE,
∴EF=$\frac{3}{2}$CF,
∴$\frac{BC}{DE}=\frac{CD}{DE}=\frac{CF}{EF}=\frac{2}{3}$,
在RT△CDE中,tan∠DCE=$\frac{DE}{CD}=\frac{3}{2}$.
故答案为:$\frac{1}{2}$或$\frac{3}{2}$.
点评 本题主要考查相似形的判定与性质及正方形的性质,根据DE的长短分类讨论是前提也是容易忽略的,利用三角形相似证明线段的长度比是切入点也是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
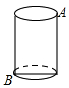 如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$.
如图是一只地面半径为2cm、高为6cm的圆柱体玻璃杯,A处有一只蚂蚁,B处有一堆残留的糖渣,蚂蚁要想吃到糖渣,它最短应爬行$\sqrt{36+4{π}^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
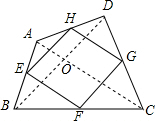 已知点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,若四边形EFGH为正方形,则原四边形ABCD应具备什么条件?说明你判断的理由.
已知点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,若四边形EFGH为正方形,则原四边形ABCD应具备什么条件?说明你判断的理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
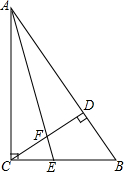 如图,在△ABC中,∠ACB=90°,∠CAB=30°,AE是△ABC的角平分线,CD是高,AE与CD相交于F点.若BE=4,则DF的长是( )
如图,在△ABC中,∠ACB=90°,∠CAB=30°,AE是△ABC的角平分线,CD是高,AE与CD相交于F点.若BE=4,则DF的长是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2{a^2}}$ | D. | $\sqrt{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com