
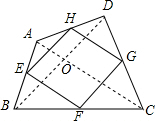
 已知点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,若四边形EFGH为正方形,则原四边形ABCD应具备什么条件?说明你判断的理由.
已知点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,若四边形EFGH为正方形,则原四边形ABCD应具备什么条件?说明你判断的理由. 分析 根据三角形的中位线平行于第三边并等于第三边的一半,先判断出AC=BD,又正方形的四个角都是直角,可以得到正方形的邻边互相垂直,然后证出AC与BD垂直,即可得到四边形ABCD满足的条件.
解答 答:当四边形ABCD满足AC=BD且AC⊥BD时,四边形EFGH为正方形,
证明:∵E、F分别是四边形ABCD的边AB、BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
同理,EH∥BD,EH=$\frac{1}{2}$BD,GF=$\frac{1}{2}$BD,GH=$\frac{1}{2}$AC,
∵AC=BD,
∴EF=EH=GH=GF,
∴平行四边形ABCD是菱形.
∵AC⊥BD,
∴EF⊥EH,
∴四边形EFGH是正方形.
点评 本题考查的是三角形的中位线定理、菱形的判定、矩形的性质与正方形的判定.解题时注意中点四边形的判定:一般中点四边形是平行四边形;如果对角线相等,则得到的中点四边形是菱形,如果对角线互相垂直,则得到的中点四边形是矩形,如果对角线相等且互相垂直,则得到的中点四边形是正方形.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
 要为一幅长30cm、宽24cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的$\frac{19}{80}$,镜框边的宽度应是多少厘米?
要为一幅长30cm、宽24cm的照片配一个镜框,要求镜框的四条边宽度相等,且镜框所占面积为照片面积的$\frac{19}{80}$,镜框边的宽度应是多少厘米?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
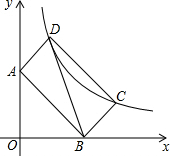 如图,在平面直角坐标系中,矩形ABCD的边AB所在直线的解析式为y=kx+2,顶点C、D在反比例函数y=$\frac{m}{x}$(m>0)的图象上,若tan∠ADB=2.则点D的坐标为(1,3).
如图,在平面直角坐标系中,矩形ABCD的边AB所在直线的解析式为y=kx+2,顶点C、D在反比例函数y=$\frac{m}{x}$(m>0)的图象上,若tan∠ADB=2.则点D的坐标为(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,以点D为圆心,DC为半径作圆弧$\widehat{CE}$,点F在边BC上,AF切$\widehat{CE}$于点E.
如图,在矩形ABCD中,以点D为圆心,DC为半径作圆弧$\widehat{CE}$,点F在边BC上,AF切$\widehat{CE}$于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com