
【题目】如图,在平面直角坐标系![]() 中,边长为
中,边长为![]() 的正方形
的正方形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴正半轴、
轴正半轴、![]() 轴的负半轴上,二次函数
轴的负半轴上,二次函数![]() 的图象经过
的图象经过![]() 、
、![]() 两点.
两点.

![]() 求该二次函数的顶点坐标;
求该二次函数的顶点坐标;
![]() 结合函数的图象探索:当
结合函数的图象探索:当![]() 时
时![]() 的取值范围;
的取值范围;
![]() 设
设![]() ,且
,且![]() ,
,![]() 两点都在该函数图象上,试比较
两点都在该函数图象上,试比较![]() 、
、![]() 的大小,并简要说明理由.
的大小,并简要说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是( )

A.6B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】岳阳王家河流域综合治理工程已正式启动,其中某项工程,若由甲、乙两建筑队合做,6个月可以完成,若由甲、乙两队独做,甲队比乙队少用5个月的时间完成.
(1)甲、乙两队单独完成这项工程各需几个月的时间?
(2)已知甲队每月施工费用为15万元,比乙队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲队做a个月,乙队做b个月(a、b均为整数)分工合作的方式施工,问有哪几种施工方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象经过(0,3),(4,3).
(1)求b、c的值.
(2)开口方向 ,对称轴为 ,顶点坐标为 .
(3)该函数的图象怎样由y=x2的图象平移得到.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的均匀转盘![]() ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘![]() ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).

【1】用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
【2】小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于X,Y定义一种新运算F,F(X,Y)=aX+2bY﹣1(其中a,b均为非零常数),这里等式右边是通常的四则运算;例如:F(2,1)=2a+2b﹣1;
(1)F(1,1)=3,F(2,﹣1)=1;
①求a和b的值;
②若关于m的不等式组![]() 只有三个整数解,求实数k的取值范围;
只有三个整数解,求实数k的取值范围;
(2)若F(X,Y)=F(Y,X)对于任意实数X,Y都成立(这里F(X,Y)和F(Y,X)均有意义),求a与b满足的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
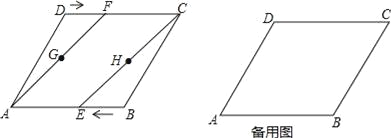
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共20只,某学习小组作摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表示活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
请估算口袋中白球约是( )只.
A. 8 B. 9 C. 12 D. 13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com