
【题目】对于X,Y定义一种新运算F,F(X,Y)=aX+2bY﹣1(其中a,b均为非零常数),这里等式右边是通常的四则运算;例如:F(2,1)=2a+2b﹣1;
(1)F(1,1)=3,F(2,﹣1)=1;
①求a和b的值;
②若关于m的不等式组![]() 只有三个整数解,求实数k的取值范围;
只有三个整数解,求实数k的取值范围;
(2)若F(X,Y)=F(Y,X)对于任意实数X,Y都成立(这里F(X,Y)和F(Y,X)均有意义),求a与b满足的关系式.
【答案】(1)①a=2,b=1;②﹣9≤k<﹣5;(2)a=2b.
【解析】
(1)①根据定义的新运算T,列出二元一次方程组,解方程组求出a,b的值;
②根据(1)求出的a,b的值和新运算列出方程组求出m的取值范围,根据题意列出不等式,解不等式求出实数k的取值范围;
(2)根据新运算列出等式,得到(a-2b)(X-Y)=0,根据题意求出a,b应满足的关系式.
(1)①![]() ,
,
解得,![]() ;
;
②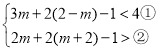 ,
,
解得![]() <m<1,
<m<1,
因为原不等式组有3个整数解,
所以﹣3≤![]() <﹣2,
<﹣2,
解得,﹣9≤k<﹣5;
(2)T(X,Y)=aX+2bY﹣1,T(Y,X)=aY+2bX﹣1,
所以aX+2bY﹣1=aY+2bX﹣1,
所以(a﹣2b)(X﹣Y)=0
所以a=2b.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】下面是某同学在一次测验中解答的填空题:①若x2=a2,则x=a;②方程2x(x-1)-x+1=0的解是x=1;③已知三角形两边分别为2和9,第三边长是方程x2-14x+48=0的根,则这个三角形的周长是17或19.其中答案完全正确的题目个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
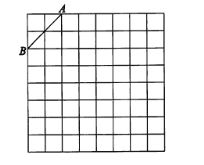
【题目】如图,是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在(1)的前提下,在第二象限内的格点上找一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点的坐标是;
(3)求((2)中△ABC的周长(结果保留根号);
(4)画出((2)中△ABC关于y轴对称的△A'B'C'.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,边长为
中,边长为![]() 的正方形
的正方形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴正半轴、
轴正半轴、![]() 轴的负半轴上,二次函数
轴的负半轴上,二次函数![]() 的图象经过
的图象经过![]() 、
、![]() 两点.
两点.

![]() 求该二次函数的顶点坐标;
求该二次函数的顶点坐标;
![]() 结合函数的图象探索:当
结合函数的图象探索:当![]() 时
时![]() 的取值范围;
的取值范围;
![]() 设
设![]() ,且
,且![]() ,
,![]() 两点都在该函数图象上,试比较
两点都在该函数图象上,试比较![]() 、
、![]() 的大小,并简要说明理由.
的大小,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() 。
。
(1)请画出![]() 关于
关于![]() 轴对称后得到的
轴对称后得到的![]() ;
;
(2)直接写出点![]() ,点
,点![]() ,点
,点![]() 的坐标;
的坐标;
(3)在![]() 轴上寻找一个点
轴上寻找一个点![]() ,使
,使![]() 的周长最小,并直接写出
的周长最小,并直接写出![]() 的周长的最小值。
的周长的最小值。

查看答案和解析>>
科目:初中数学 来源: 题型:
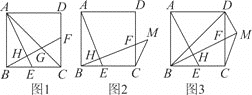
【题目】已知正方形ABCD中,点E,F分别为BC,CD上的点,连接AE,BF相交于点H,且AE⊥BF.
(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;
(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH=BM;
(3)如图3,在(2)的条件下,若点H为BM的三等分点,连接BD,DM,若HE=1,求△BDM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,∠C=70°,∠B=∠D=90°,E、F 分别是 BC、DC 上的点,当△AEF 的周长最小时,∠EAF 的度数为()

A.30°B.40°C.50°D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.
(1)判断CM与⊙O的位置关系,并说明理由;
(2)若∠ECF=2∠A,CM=6,CF=4,求MF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com