
【题目】在菱形ABCD中,∠B=60,E是边CD上一点,以CE为边作等边△CEF.
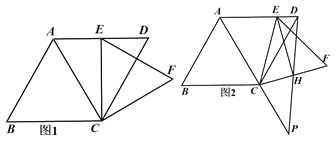
(1) 如图1,当CE⊥AD ,CF=![]() 时,求菱形ABCD的面积;
时,求菱形ABCD的面积;
(2) 如图2,过点E作∠CEF的平分线交CF于H,连接DH,并延长DH与AC的延长交于点P,若∠ECD=15,求证:![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由等边三角形的性质得出CE的长.再由菱形的性质及∠B=60得到CD的长,根据菱形的面积公式即可得出结论.
(2)连接DF,过F作FG⊥CD于G.由菱形的性质及∠B=60得到△ABC和△ACD是等边三角形,即可证明△ACE≌△DCF,进而得到DF//AP,由平行线的性质得到∠FDH=∠CPH.
由等边三角形的性质得到CH=HF.可证明△CHP≌△FHD,得到DF=CP.在Rt△DGF中,由∠FDC=60,可得![]() .在等腰Rt△CFG中,有
.在等腰Rt△CFG中,有![]() ,从而可以得出结论.
,从而可以得出结论.
(1)∵等边△CEF,CF=![]() ,∴CE=CF=
,∴CE=CF=![]() .
.
∵菱形ABCD,∠B=60,∴∠D=∠B=60,AD=CD.
∵CE⊥AD,∴∠ECD=30,∴CD=4,∴AD=4,∴S菱形ABCD=ADCE=![]() .
.
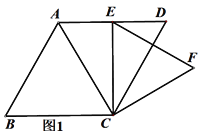
(2)连接DF,过F作FG⊥CD于G.
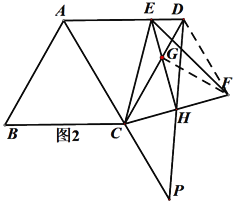
∵菱形ABCD,∴AB=BC=CD=AD.
∵∠B=60,∴△ABC和△ACD是等边三角形,∴∠CAD=∠ACD=60.
∵等边△CEF,∴CE=CF,∠ECF=60,∴∠ACD-∠ECD=∠ECF-∠ECD即∠ACE=∠DCF.
在△ACE与△DCF中,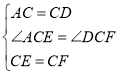 ,∴△ACE≌△DCF,∴∠FDC=60.
,∴△ACE≌△DCF,∴∠FDC=60.
∵∠ACD=60,∴DF//AP,∴∠FDH=∠CPH.
∵等边△CEF,EH平分∠CEF,∴CH=HF.
在△CHP与△FHD中,∵∠FDH=∠CPH,∠FHD=∠CHP,HF=CH,∴△CHP≌△FHD,∴DF=CP.
∵∠FDC=60,FG⊥CD,∴![]() .
.
∵∠ECF=60,∠ECD=15,∴∠DCF=45.
∵∠DCF=45,FG⊥CD,∴![]() ,∴
,∴![]() .
.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=2,BC=4.点D是线段BC上的一个动点.点D与点B、C不重合,过点D作DE⊥BC交AB于点E,将△ABC沿着直线DE翻折,使点B落在直线BC上的F点.
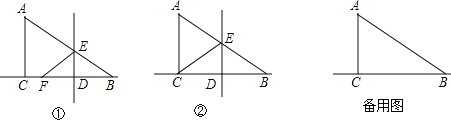
(1)设∠BAC=α(如图①),求∠AEF的大小;(用含α的代数式表示)
(2)当点F与点C重合时(如图②),求线段DE的长度;
(3)设BD=x,△EDF与△ABC重叠部分的面积为S,试求出S与x之间函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市拟调整出租车运价,调整方案见下列表格及图象(其中![]() 为常数)
为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过 | 起步价7元 | 起步价 |
超过 | 每公里2元 | 每公里 |
超出 | 每公里 | |
设行驶路程为![]() ,调价前的运价
,调价前的运价![]() (元),调价后运价
(元),调价后运价![]() (元),如图,折线
(元),如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系式,线段
之间的函数关系式,线段![]() 表示当
表示当![]() 时,
时,![]() 与
与![]() 的函数关系式,根据图表信息,完成下列各题:
的函数关系式,根据图表信息,完成下列各题:
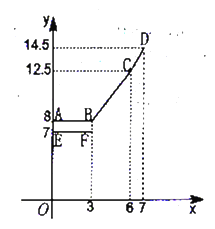
①填空:![]() ,
,![]() ,
,![]() ;
;
②当![]() 时,求
时,求![]() 与
与![]() 的关系,补充图中该函数的图像;
的关系,补充图中该函数的图像;
③函数![]() 与
与![]() 的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
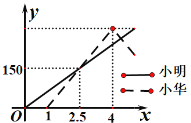
【题目】小明和小华先后从甲地出发到乙地,小明先乘坐客车出发1小时,小华才开车前住乙地,小华到达乙地后立即按原速从乙地返回甲地。已知小明、小华离甲地距离y(千米)与小明出发时间x(小时)之间的函数关系如图所示,请根据图象解答下列问题:小华从乙地返回后再经过___小时与小明相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
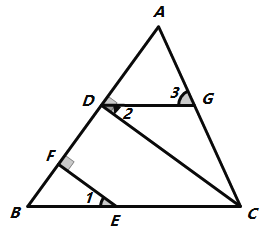
【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨.第一批蒜薹价格为4000元/吨;因蒜薹大量上市,第二批价格跌至1000元/吨.这两批蒜薹共用去16万元.
(1)求两批次购进蒜薹各多少吨;
(2)公司收购后对蒜薹进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
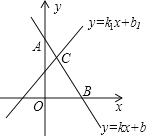
【题目】在数学学习中,及时对知识进行归纳和整理是提高学习效率的重要方法,善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对照图形,把相关知识归纳整理如下:
一次函数与方程(组)的关系:
(1)一次函数的解析式就是一个二元一次方程;
(2)点B的横坐标是方程kx+b=0的解;
(3)点C的坐标(x,y)中x,y的值是方程组①的解.
一次函数与不等式的关系:
(1)函数y=kx+b的函数值y大于0时,自变量x的取值范围就是不等式kx+b>0的解集;
(2)函数y=kx+b的函数值y小于0时,自变量x的取值范围就是不等式②的解集.
(一)请你根据以上归纳整理的内容在下面的数字序号后写出相应的结论:① ;② ;
(二)如果点B坐标为(2,0),C坐标为(1,3);
①直接写出kx+b≥k1x+b1的解集;
②求直线BC的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
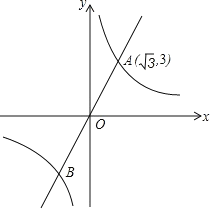
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点,且点A的横坐标为
的图象交于A,B两点,且点A的横坐标为![]() .在坐标轴上找一点C,直线AB上找一点D,在双曲线y=
.在坐标轴上找一点C,直线AB上找一点D,在双曲线y=![]() 找一点E,若以O,C,D,E为顶点的四边形是有一组对角为60的菱形,那么符合条件点D的坐标为___.
找一点E,若以O,C,D,E为顶点的四边形是有一组对角为60的菱形,那么符合条件点D的坐标为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com