
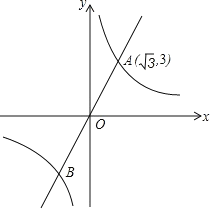
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点,且点A的横坐标为
的图象交于A,B两点,且点A的横坐标为![]() .在坐标轴上找一点C,直线AB上找一点D,在双曲线y=
.在坐标轴上找一点C,直线AB上找一点D,在双曲线y=![]() 找一点E,若以O,C,D,E为顶点的四边形是有一组对角为60的菱形,那么符合条件点D的坐标为___.
找一点E,若以O,C,D,E为顶点的四边形是有一组对角为60的菱形,那么符合条件点D的坐标为___.
【答案】(3,3![]() )或(3,3
)或(3,3![]() ).
).
【解析】
把A的横坐标代入直线解析式求出y的值,确定出A坐标,把A坐标代入反比例解析式求出k的值,确定出反比例解析式,设D(a,![]() a),由直线AB解析式可知,直线AB与y轴正半轴夹角为60°,以O、C、D、E为顶点的四边形是有一组对角为60°的菱形,D在直线y=
a),由直线AB解析式可知,直线AB与y轴正半轴夹角为60°,以O、C、D、E为顶点的四边形是有一组对角为60°的菱形,D在直线y=![]() x上,得到点C只能在y轴上,得出E横坐标为a,把x=a代入反比例函数解析式求出y的值,确定出E坐标,由菱形的边长相等得到OD=ED,进而求出a的值,确定出满足题意D的坐标即可.
x上,得到点C只能在y轴上,得出E横坐标为a,把x=a代入反比例函数解析式求出y的值,确定出E坐标,由菱形的边长相等得到OD=ED,进而求出a的值,确定出满足题意D的坐标即可.
把x=![]() 代入y=
代入y=![]() x,得:y=3,即A(
x,得:y=3,即A(![]() ,3),
,3),

把点A(![]() ,3)代入y=kx,解得:k=3
,3)代入y=kx,解得:k=3![]() ,
,
∴反比例函数解析式为y=![]() ,
,
设D点坐标(a,![]() a),由直线AB解析式可知,直线AB与y轴正半轴夹角为60,
a),由直线AB解析式可知,直线AB与y轴正半轴夹角为60,
∵以O、C. D.E为顶点的四边形是有一组对角为60的菱形,D在直线y=![]() x上,
x上,
∴点C只能在y轴上,
∴E点的横坐标为a,
把x=a代入y=![]() ,得:y=
,得:y=![]() ,即E(a,
,即E(a, ![]() ,
,
根据OE=ED,即: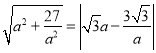 ,
,
解得:a=±3,
则满足题意D为(3,3![]() )或(3,3
)或(3,3![]() ).
).
故答案为:(3,3![]() )或(3,3
)或(3,3![]() ).
).


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠B=60,E是边CD上一点,以CE为边作等边△CEF.
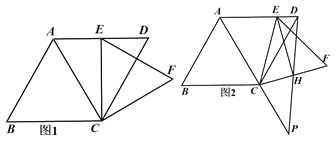
(1) 如图1,当CE⊥AD ,CF=![]() 时,求菱形ABCD的面积;
时,求菱形ABCD的面积;
(2) 如图2,过点E作∠CEF的平分线交CF于H,连接DH,并延长DH与AC的延长交于点P,若∠ECD=15,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,对角线AC、BD相交于点O,过点O作EF⊥AC分别交射线AD与射线CB于点E和点F,联结CE、AF.
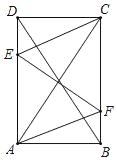
(1)求证:四边形AFCE是菱形;
(2)当点E、F分别在边AD和BC上时,如果设AD=x,菱形AFCE的面积是y,求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ODE是等腰三角形,求AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
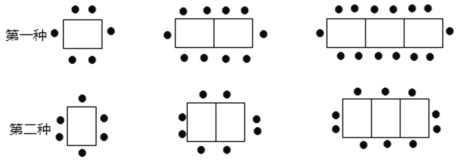
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待70位顾客共同就餐,但餐厅只有18张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校组织800名学生参加了一次“汉字听写”大赛.赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
90,92,81,82,78,95,86,88,72,66,62,68,89,86,93,83,100,73,76,80,77,81,86,75,82,85,71,68,74,98,90,97,85,84,78,73,65,92,96,60
对上述成绩进行了整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
60≤x<70 | 6 | 0.15 |
70≤x<80 | a | b |
80≤x<90 | 14 | 0.35 |
90≤x≤100 | c | d |
请根据所给信息,解答下列问题:
(1)a= ,d= .
(2)请补全频数分布直方图
(3)若成绩在90分以上(包括90分)的为“优等,请你估计参加这次比赛的800名学生中成绩“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 是⊙
是⊙![]() 上一点,
上一点, ![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分∠
平分∠![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
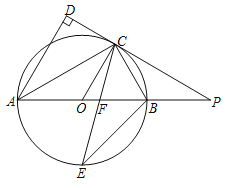
(1)求证: ![]() 平分∠
平分∠![]() ;
;
(2)求证:PC=PF;
(3)若![]() ,AB=14,求线段
,AB=14,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com