练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

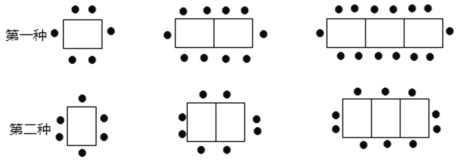
    【题目】某餐厅中，一张桌子可坐6人，有以下两种摆放方式：

    （1）当有n张桌子时，两种摆放方式各能坐多少人？

    （2）一天中午餐厅要接待70位顾客共同就餐，但餐厅只有18张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？

    【答案】（1）当有n张桌子时，第一种摆放方式能坐人，第二种摆放方式能坐人；（2）选择第一种摆放方式来摆放餐桌，见解析

    【解析】

    （1）分别探索出当有n张桌子时，第一种摆放方式和第二种摆放方式能坐的人数即可；

    （2）将n=18代入（1）中代数式，然后比较大小即可判断.

    解：（1）第一种摆放方式中：一张桌子可坐6=（4×1＋2）人；

    两张桌子可坐10=（4×2＋2）人；

    三张桌子可坐14=（4×3＋2）人；

    ∴第一种摆放方式，当有n张桌子时，能坐人；

    第二种摆放方式中：一张桌子可坐6=（2×1＋4）人；

    两张桌子可坐8=（2×2＋4）人；

    三张桌子可坐10=（2×3＋4）人；

    ∴第二种摆放方式中：当有n张桌子时，能坐人.

    （2）当时，第一种摆放方式能坐人

    第二种摆放方式能坐人

    因为

    所以应该选择第一种摆放方式来摆放餐桌.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨．第一批蒜薹价格为4000元/吨；因蒜薹大量上市，第二批价格跌至1000元/吨．这两批蒜薹共用去16万元．

    (1)求两批次购进蒜薹各多少吨；

    (2)公司收购后对蒜薹进行加工，分为粗加工和精加工两种：粗加工每吨利润400元，精加工每吨利润1000元．要求精加工数量不多于粗加工数量的三倍．为获得最大利润，精加工数量应为多少吨？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠AOB＝20°，∠AOC＝4∠AOB，OD平分∠AOB，OM平分∠AOC，则∠MOD的度数是_____________________度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分别把下列各数填在所属的集合内：

    +29，﹣3，80%，﹣1，0.3，0，﹣31415，6，

    （1）正数集合：{_____…}；

    （2）负数集合：{_____…}；

    （3）整数集合：{_____…}；

    （4）分数集合：{_____…}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

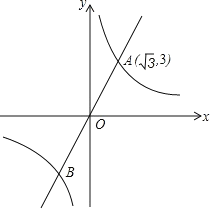
    【题目】如图,已知直线y=x与反比例函数y=的图象交于A,B两点,且点A的横坐标为.在坐标轴上找一点C,直线AB上找一点D,在双曲线y=找一点E,若以O,C,D,E为顶点的四边形是有一组对角为60的菱形，那么符合条件点D的坐标为___.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

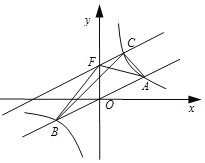
    【题目】如图，在平面直角坐标系中，直线与双曲线交于、两点，且点的坐标为，将直线向上平移个单位，交双曲线于点，交轴于点，且的面积是．给出以下结论：（1）；（2）点的坐标是；（3）；（4）．其中正确的结论有　　

    A. 1个B. 2个C. 3个D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

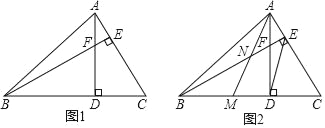
    【题目】如图1，在锐角△ABC中，∠ABC=45°，高线AD、BE相交于点F．

    （1）判断BF与AC的数量关系并说明理由；

    （2）如图2，将△ACD沿线段AD对折，点C落在BD上的点M，AM与BE相交于点N，当DE∥AM时，判断NE与AC的数量关系并说明理由．

    【答案】（1）BF=AC，理由见解析；（2）NE=AC，理由见解析.

    【解析】试题分析：（1）如图1，证明△ADC≌△BDF（AAS），可得BF=AC；
    （2）如图2，由折叠得：MD=DC，先根据三角形中位线的推论可得：AE=EC，由线段垂直平分线的性质得：AB=BC，则∠ABE=∠CBE，结合（1）得：△BDF≌△ADM，则∠DBF=∠MAD，最后证明∠ANE=∠NAE=45°，得AE=EN，所以EN=AC．

    试题解析：

    （1）BF=AC，理由是：

    如图1，∵AD⊥BC，BE⊥AC，

    ∴∠ADB=∠AEF=90°，

    ∵∠ABC=45°，

    ∴△ABD是等腰直角三角形，

    ∴AD=BD，

    ∵∠AFE=∠BFD，

    ∴∠DAC=∠EBC，

    在△ADC和△BDF中，

    ∵，

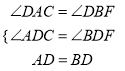    ∴△ADC≌△BDF（AAS），

    ∴BF=AC；

    （2）NE=AC，理由是：

    如图2，由折叠得：MD=DC，

    ∵DE∥AM，

    ∴AE=EC，

    ∵BE⊥AC，

    ∴AB=BC，

    ∴∠ABE=∠CBE，

    由（1）得：△ADC≌△BDF，

    ∵△ADC≌△ADM，

    ∴△BDF≌△ADM，

    ∴∠DBF=∠MAD，

    ∵∠DBA=∠BAD=45°，

    ∴∠DBA﹣∠DBF=∠BAD﹣∠MAD，

    即∠ABE=∠BAN，

    ∵∠ANE=∠ABE+∠BAN=2∠ABE，

    ∠NAE=2∠NAD=2∠CBE，

    ∴∠ANE=∠NAE=45°，

    ∴AE=EN，

    ∴EN=AC．

    【题型】解答题
    【结束】
    17

    【题目】已知x1，x2是方程2x2﹣2nx+n（n+4）=0的两根，且（x1﹣1）（x2﹣1）﹣1=，求n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某区为争创全国文明卫生城，2016年区政府对区绿化工程投入的资金是2000万元，2018年投的资金是2420万元，且2017年和2018年，每年投入资金的年平均增长率相同．

    （1）求该区对区绿化工程投入资金的年平均增长率；

    （2）若投入资金的年平均增长率不变，那么该区在2020年需投入资金多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：在直角坐标系中，A（﹣2，4）B（﹣4，2）；A1、B1是A、B关于y轴的对称点；

    （1）请在图中画出A、B关于原点O的对称点A2，B2（保留痕迹，不写作法）；并直接写出A1、A2、B1、B2的坐标．

    （2）试问：在x轴上是否存在一点C，使△A1B1C的周长最小，若存在求C点的坐标，若不存在说明理由．

    查看答案和解析>>

    同步练习册答案