
分析 由9π≈28.26,可得其整数部分a=28,由27<28<64,可得$\root{3}{27}$<$\root{3}{28}$<$\root{3}{64}$,可得3$<\root{3}{28}$<4,可得$\root{3}{28}$的小数部分b=$\root{3}{28}$-3,可得a+b的值.
解答 解:∵9π≈28.26,
∴a=28,
∵27<28<64,
∴$\root{3}{27}$<$\root{3}{28}$<$\root{3}{64}$,
∴3$<\root{3}{28}$<4,
∴b=$\root{3}{28}$-3,
∴a+b=28+$\root{3}{28}$-3=25$+\root{3}{28}$,
∴a+b的值为25$+\root{3}{28}$.
点评 本题主要考查了估算无理数的大小,根据题意估算出a,b的值是解答此题的关键.


科目:初中数学 来源: 题型:解答题
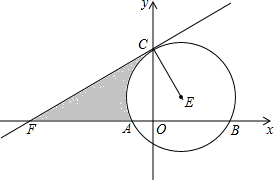 如图,半径为2的⊙E交x轴于A、B,交y轴于点C、D,直线CF交x轴负半轴于点F,连接EC.已知点E的坐标为(1,1),∠OFC=30°.
如图,半径为2的⊙E交x轴于A、B,交y轴于点C、D,直线CF交x轴负半轴于点F,连接EC.已知点E的坐标为(1,1),∠OFC=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果两条直线都与第三条直线平行,那么这两条直线也互相平行 | |
| B. | 两条直线被第三条直线所截,同旁内角互补 | |
| C. | 两直线平行,内错角相等 | |
| D. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
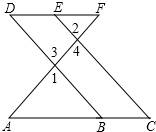 完成下面的证明.
完成下面的证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| X(元/件) | 35 | 40 | 45 | 50 | 55 |
| Y(件) | 550 | 500 | 450 | 400 | 350 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com