
����Ŀ����֪��������![]() �ύ��
�ύ��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
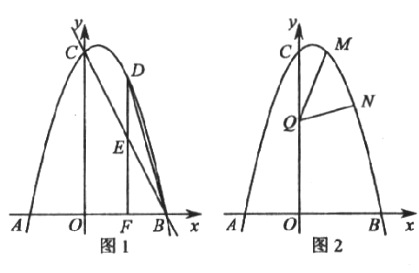
��1����������ߵı���ʽ����������ꣻ
��2������![]() ��
��![]() ���Ϸ��������ϵ�һ�����㣨���
���Ϸ��������ϵ�һ�����㣨���![]() ���غϣ�������
���غϣ�������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() .���
.���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() .
.
�����ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���
�ij���
��ֱ��![]() �ܷ��
�ܷ��![]() �ֳ����֮��Ϊ1��2�������֣����ܣ��������
�ֳ����֮��Ϊ1��2�������֣����ܣ��������![]() �����ꣻ�����ܣ���˵������.
�����ꣻ�����ܣ���˵������.
��3����ͼ2������![]() Ҳ�ڴ��������ϣ�����
Ҳ�ڴ��������ϣ�����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �������ڣ���ֱ��д����
�������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
���𰸡���1��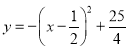 ����������Ϊ��
������������![]() ����2����
����2����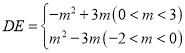 �����ܣ����ɼ���������
�����ܣ����ɼ���������![]() ������Ϊ
������Ϊ![]() ����3�����ڣ���Q������Ϊ��
����3�����ڣ���Q������Ϊ��![]() ��
��![]() .
.
��������
��1�����ݴ���ϵ����������������ߵĽ���ʽ��Ȼ���һ��ʽת��Ϊ����ʽ���ɵó������ߵĶ������ꣻ
��2���������ô���ϵ�������ֱ��![]() �ĺ�������ʽ���������D��E�����꣬Ȼ��ֵ�D��y���Ҳ��y���������
�ĺ�������ʽ���������D��E�����꣬Ȼ��ֵ�D��y���Ҳ��y���������![]() ��
��![]() ��ʽ���ɣ�
��ʽ���ɣ�
���������������жϣ���D��y�����ʱ�������������ĵ�![]() ������D��y���Ҳ�ʱ����
������D��y���Ҳ�ʱ����![]() ��
��![]() ������������E��F������г�������⼴�ɣ�
������������E��F������г�������⼴�ɣ�
��3������õ�M��N�����꣬Ȼ������CM������N��NG��CM��CM���ӳ����ڵ�G�������ж���MCN=45�������C��Ϊ���������һ����Q��������һ������ĵ�QӦΪ����C��M��N�ġ�H��y��Ľ��㣬Ȼ�����Բ�ܽǶ��������ۡ�����ֱ�������ε����ʺ��ɶ����������CQ�ij��������ɵý��.
�⣺��1������������![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
���������ߵı���ʽΪ��![]() ��
��
�ѵ�![]() ���벢��ã�
���벢��ã�![]() ��
��
�������ߵı���ʽΪ��![]()
![]() ��
��
��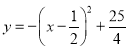 ���������ߵĶ�������Ϊ��
���������ߵĶ�������Ϊ��![]() ��
��
��2������ֱ��![]() �ı���ʽΪ��
�ı���ʽΪ��![]() ����
����![]() ����ã�
����ã�![]() ��
��
��ֱ��![]() �ı���ʽΪ��
�ı���ʽΪ��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ʱ����
ʱ����![]()
![]() ��
��
��![]() ʱ��
ʱ��![]()
![]() ��
��
���ϣ�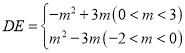 ��
��
��������֪����![]() ʱ�������������ĵ�
ʱ�������������ĵ�![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() �����
�����![]() ����ȥ������
����ȥ������![]() ��
��
��![]() �����
�����![]() ����ȥ����
����ȥ����![]() ����ȥ����
����ȥ����
���ϣ�ֱ��![]() �ܰ�
�ܰ�![]() �ֳ����֮��Ϊ1��2�������֣��ҵ�
�ֳ����֮��Ϊ1��2�������֣��ҵ�![]() ������Ϊ
������Ϊ![]() ��
��
��3���ߵ�![]() ��������
��������![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��
����MC����ͼ����C��0��6����M��1��6����MC��y�ᣬ����N��NG��CM��CM���ӳ����ڵ�G����N��2��4������CG=NG=2�����CNG�ǵ���ֱ�������Σ����MCN=45�������C��Ϊ���������һ����Q������һ������ĵ�QӦΪ����C��M��N�ġ�H��y��Ľ��㣬����HN��
��![]() ����MN=
����MN=![]() ��CM=1��
��CM=1��
��![]() �����MHN=90������뾶MH=NH=
�����MHN=90������뾶MH=NH=![]() ��
��
����MCQ=90������MQ��ֱ������![]() ����
����![]() ��
��
��OC=6����OQ=3����Q��0��3����
���ϣ���![]() ���ϴ��ڵ�
���ϴ��ڵ�![]() ��ʹ
��ʹ![]() ���ҵ�Q������Ϊ��
���ҵ�Q������Ϊ��![]() ��
��![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
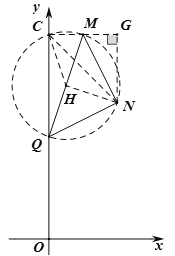
����Ŀ��������y��ax2+bx+c��a��0���Գ���Ϊֱ��x����1���䲿��ͼ����ͼ��ʾ�������н��ۣ�
��b2��4ac��0��
��2a��b��
��t��at+b����a��b��tΪ����ʵ������
��3b+2c��0��
�ݵ㣨��![]() ��y1������
��y1������![]() ��y2������
��y2������![]() ��y3���Ǹ��������ϵĵ㣬��y1��y3��y2��
��y3���Ǹ��������ϵĵ㣬��y1��y3��y2��
������ȷ���۵ĸ����ǣ�������
A.5B.4C.3D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�A��ת������AB��C��D��λ�ã���ʱAC�����е�ǡ����D���غϣ�AB����CD�ڵ�E����AB��6��
��1��BC��_____��
��2����AEC�����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() �����ģ�
�����ģ�![]() ��
��![]() ��
��![]() ����һ�㣬�Ե�
����һ�㣬�Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��
Ϊ�뾶��![]() ������
������![]() ����
����![]() �ڵ�
�ڵ�![]() .
.
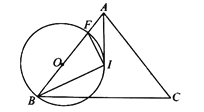
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2������![]() ����
����![]() ��
��![]() ����Բ��
����Բ��![]() ��
��![]() �ľ��뼰
�ľ��뼰![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��������������ֱ�Ϊ
��������������ֱ�Ϊ![]() .
.
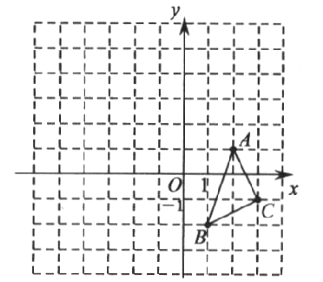
��1������![]() ��ʹ
��ʹ![]() ��
��![]() ���ڵ�
���ڵ�![]() �����ĶԳƣ���д����
�����ĶԳƣ���д����![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ������_____________��
������_____________��
��2����ԭ��![]() Ϊλ�����ģ�λ�Ʊ�Ϊ1��2����
Ϊλ�����ģ�λ�Ʊ�Ϊ1��2����![]() �����࣬������
�����࣬������![]() �Ŵ���
�Ŵ���![]() ����д����
����д����![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ������___________________��
������___________________��
��3��![]() ___________________.
___________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
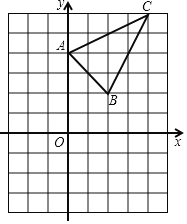
����Ŀ����ͼ����ABC������ƽ���ڣ��������������ֱ�ΪA��0��4����B��2��2����C��4��6���������������У�ÿ��С�����εı߳�Ϊ1��
��1��������ABC����ƽ��5����λ�õ��ġ�A1B1C1����д����B1�����ꣻ
��2���Ե�OΪλ�����ģ��ڵ�����������A2B2C2��ʹ��A2B2C2���ABCλ�ƣ���λ�Ʊ�Ϊ1��2��ֱ��д����C2������͡�A2B2C2�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
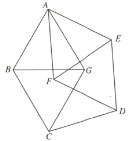
����Ŀ����ͼ��ʾ��ƽ�����߸���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ͼ�����е����߳�����ȣ���
��ͼ�����е����߳�����ȣ���![]() ______.
______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P����C���������¶��壺����PC����C�ڵ�N������P���ڵ�N�ĶԳƵ�Q����C���ڲ�����Ƶ�P����C����Ƶ㣮
��1������O�İ뾶Ϊ1ʱ��
���ڵ�D����1����1����E��2��0����F��0��4���У���O����Ƶ����� ����
������M��m��n��Ϊ��O����Ƶ㣬���߶�MO����O�ڵ�G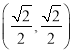 ����m��ȡֵ��Χ��
����m��ȡֵ��Χ��
��2��ֱ��y����x+b����A��1��1������x�ύ�ڵ�B����T��Բ��ΪT��t��0�����뾶Ϊ1�����߶�AB�ϵ����е㶼����T����Ƶ㣬��ֱ��д��t��ȡֵ��Χ��
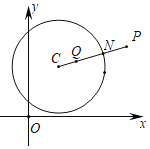
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ͼ��Ķ���Ϊ
ͼ��Ķ���Ϊ![]() ����ͼ����
����ͼ����![]() ��Ľ���
��Ľ���![]() ��
��![]() �ĺ�����ֱ�Ϊ
�ĺ�����ֱ�Ϊ![]() ��
��![]() ����
����![]() �Ḻ���ύ�ڵ�
�Ḻ���ύ�ڵ�![]() ����������������У�
�����������������
��![]() ����
����![]() ����
����![]() ����ֻ�е�
����ֻ�е�![]() ʱ��
ʱ��![]() �ǵ���ֱ�������Σ���ʹ
�ǵ���ֱ�������Σ���ʹ![]() Ϊ���������ε�
Ϊ���������ε�![]() ֵ�������ĸ���
ֵ�������ĸ���
������ȷ�Ľ����У� ��

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com