
【题目】在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2017OB2017.则点B2017的坐标是____________.

【答案】(22017,-22017)
【解析】
根据题意得出B点坐标变化规律,进而得出点B2017的坐标位置,进而得出答案.
∵△AOB是等腰直角三角形,OA=1,
∴AB=OA=1,
∴B(1,1),
将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,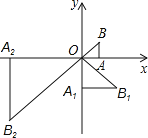
再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,
∴每4次循环一周,B1(2,-2),B2(-4,-4),B3(-8,8),B4(16,16),
∵2017÷4=503…1,
∴点B2017与B1同在一个象限内,
∵-4=-22,8=23,16=24,
∴点B2017(22017,-22017).
故答案为:(22017,-22017).


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5cm,水面宽AB为8cm,则水的最大深度CD为( ) 
A.4cm
B.3cm
C.2cm
D.1cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知反比例函数y= ![]() 的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(﹣2,﹣8),一次函数y=ax+b与x轴交于点A,与y轴交于点B.
的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(﹣2,﹣8),一次函数y=ax+b与x轴交于点A,与y轴交于点B. 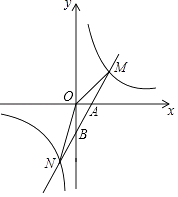
(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于![]() EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )

A. 120° B. 30° C. 150° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.

(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③ 2S四边形AEPF=S△ABC;④EF=PC.上述结论正确的有 ( ).
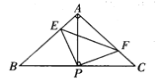
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将半径为3cm,圆心角为60°的扇形纸片.AOB在直线l上向右作无滑动的滚动至扇形A′O′B′处,则顶点O经过的路线总长 cm(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com