
【题目】如图,△ABC中,AD⊥BC于D,若BD=AD,FD=CD.猜想:BF与AC的关系,并证明.

【答案】BF=AC且BF⊥AC,证明见解析.
【解析】试题分析: 首先求出∠ADC=∠BDF=90°,根据SAS证△ADC≌△BDF,根据全等三角形的性质推出FB=AC;根据三角形的内角和定理求出∠FBD+∠BFD=90°,推出∠AFE+∠EAF=90°,在△AFE中,根据三角形的内角和定理求出∠AEF=90°,可得BF⊥AC.
解:BF=AC且BF⊥AC.
∵AD⊥BC,
∴∠ADC=∠BDF=90°,
∵在△ADC和△BDF中,
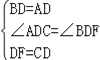 ,
,
∴△ADC≌△BDF(SAS),
∴∠FBD=∠CAD,
BF=AC;
∵∠BDF=90°,
∴∠FBD+∠BFD=90°,
∵∠AFE=∠BFD,
由(1)知:∠FBD=∠CAD,
∴∠CAD+∠AFE=90°,
∴∠AEF=180°﹣(∠CAD+∠AFE)=90°,
∴BF⊥AC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,AB∥CD,直线EF分别交AB,CD于点G,H,GM,HN分别为∠BGE和∠DHG的平分线.
(1)试判断GM和HN的位置关系;
(2)如果GM是∠AGH的平分线,(1)中的结论还成立吗?
(3)如果GM是∠BGH的平分线,(1)中的结论还成立吗?如果不成立,你能得到什么结论?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正比例函数y=k1x与反比例函数![]() 交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.
交于点A,从A向x轴、y轴分别作垂线,所构成的正方形的面积为4.
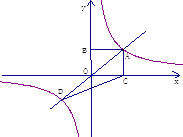
(1)分别求出正比例函数与反比例函数的解析式;
(2)求出正、反比例函数图象的另外一个交点坐标。
(3)求△ODC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠ABC=64°,∠AEB=70°.
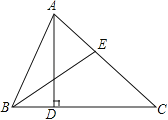
(1)求∠CAD的度数;
(2)若点F为线段BC上的任意一点,当△EFC为直角三角形时,求∠BEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)仔细观察,在图2中有 个以线段AC为边的“8字形”;
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究应用:用“∪”、“∩”定义两种新运算:对于两数a、b,规定a∪b=10a×10b,a∩b=10a÷10b,例如:3∪2=103×102=105,3∩2=103÷102=10.
(1) 求: (2017∪983) 的值
(2) 求: (2018∩2016) 的值;
(3) 当x为何值时, (x∪5)的值与 (23∩17)的值相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.

(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列事件发生的概率,把A,B,C,D填入事件后的括号里.
A.发生的概率为0 B.发生的概率小于![]()
C.发生的概率大于![]() D.发生的概率为1
D.发生的概率为1
(1)从一副扑克牌中任意抽取一张,是红桃;( )
(2)2024年2月有29天;( )
(3)小波能举起500 kg的大石头;( )
(4)从5张分别写有数字1,2,4,6,8的卡片中任取一张,卡片上数字恰为偶数.( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com