【题目】如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．
（1）求证：△BDE∽△BAC；
（2）已知AC=6，BC=8，求线段AD的长度．
【答案】（1）证明见解析；（2）3
.
【解析】试题分析：(1)、根据折叠得出∠C=∠BED=90°，结合∠B为公共角得出三角形相似；(2)、首先求出AB的长度，然后设CD=x，根据折叠得出DE和BE的长度，从而根据Rt△BDE的勾股定理求出DE的长度，然后根据Rt△ADE的勾股定理求出AD的长度.
试题解析：(1)、∵∠C=90° 根据折叠图形的性质 ∴∠BED=90° ∴∠C=∠BED 又∵∠B=∠B
∴△BDE∽△BAC
(2)、根据Rt△ABC的勾股定理可得AB=10，设CD=x，则BD=8－x，DE=x，AE=AC=6，则BE=10，
根据Rt△BDE的勾股定理可得：DE=3， 根据Rt△ADE的勾股定理可得：AD=3
计算高手系列答案科目：初中数学 来源： 题型：
【题目】某市公交快速通道开通后，为响应市政府“绿色出行”的号召，家住新城的小王上班由自驾车改为乘坐公交车．已知小王家距上班地点18千米，他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米，他从家出发到达上班地点，乘公交车方式所用时间是自驾车方式所用时间的
．小王用自驾车方式上班平均每小时行驶多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明和小红学习了用图形面积研究整式乘法的方法后，分别进行了如下数学探究：把一根铁丝截成两段，
探究1：小明截成了两根长度不同的铁丝，并用两根不同长度的铁丝分别围成两个正方形，已知两正方形的边长和为20cm，它们的面积的差为40cm2，则这两个正方形的边长差为________；
探究2：小红截成了两根长度相同的铁丝，并用两根同样长的铁丝分别围成一个长方形与一个正方形，若长方形的长为xcm，宽为ycm.
(1)用含x，y的代数式表示正方形的边长为________；
(2)设长方形的长大于宽，比较正方形与长方形面积哪个大，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场用24000元购入一批空调，然后以每台3000元的价格销售，因天气炎热，空调很快售完；商场又以52000元的价格再次购入该种型号的空调，数量是第一次购入的2倍，但购入的单价上调了200元，售价每台也上调了200元．
（1）商场第一次购入的空调每台进价是多少元？
（2）商场既要尽快售完第二次购入的空调，又要在这两次空调销售中获得的利润率不低于22%，打算将第二次购入的部分空调按每台九五折出售，最多可将多少台空调打折出售？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若∠C=α，∠EAC+∠FBC=β
（1）如图①，AM是∠EAC的平分线，BN是∠FBC的平分线，若AM∥BN，则α与β有何关系？并说明理由．
（2）如图②，若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P，试探究∠APB与α、β的关系是______．（用α、β表示）
（3）如图③，若α≥β，∠EAC与∠FBC的平分线相交于P1，∠EAP1与∠FBP1的平分线交于P2 ；依此类推，则∠P5=______．（用α、β表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＝BC，∠ABC＝90°，BM是AC边上的中线，点D，E分别在边AC和BC上，DB＝DE，DE与BM相交于点N，EF⊥AC于点F，以下结论：
①∠DBM＝∠CDE；②S△BDE<S四边形BMFE；③CD·EN＝BN·BD；④AC＝2DF.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
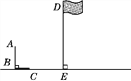
【题目】如图，九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度，已知直立在地面上的竹竿AB的长为3 m．某一时刻，测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影，并写出画图步骤；
(2)在测量竹竿AB的影长时，同时测得旗杆DE在阳光下的影长为6 m，请你计算旗杆DE的高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
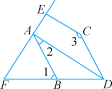
【题目】如图，已知∠1=∠BDC，∠2+∠3=180°．
（1）请你判断DA与CE的位置关系，并说明理由；
（2）若DA平分∠BDC，CE⊥AE于E，∠1=70°，试求∠FAB的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
