
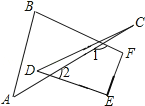
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)仔细观察,在图2中有 个以线段AC为边的“8字形”;
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .

【答案】360°
【解析】
试题分析:(1)以M为交点的“8字形”有1个,以O为交点的“8字形”有2个;
(2)根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C﹣∠P=∠P﹣∠B,即∠P=![]() (∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;
(∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;
(3)与(2)的证明方法一样得到∠P=![]() (2∠C+∠B).
(2∠C+∠B).
(4)根据三角形内角与外角的关系可得∠B+∠A=∠1,∠C+∠D=∠2,再根据四边形内角和为360°可得答案.
解:(1)在图2中有3个以线段AC为边的“8字形”,
故答案为3;
(2)∵∠CAB和∠BDC的平分线AP和DP相交于点P,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C﹣∠P=∠P﹣∠B,
即∠P=![]() (∠C+∠B),
(∠C+∠B),
∵∠C=100°,∠B=96°
∴∠P=![]() (100°+96°)=98°;
(100°+96°)=98°;
(3)∠P=![]() (β+2α);
(β+2α);
理由:∵∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,
∠CDB,
∴∠BAP=![]() ∠BAC,∠BDP=
∠BAC,∠BDP=![]() ∠BDC,
∠BDC,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C﹣∠P=![]() ∠BDC﹣
∠BDC﹣![]() ∠BAC,∠P﹣∠B=
∠BAC,∠P﹣∠B=![]() ∠BDC﹣
∠BDC﹣![]() ∠BAC,
∠BAC,
∴2(∠C﹣∠P)=∠P﹣∠B,
∴∠P=![]() (∠B+2∠C),
(∠B+2∠C),
∵∠C=α,∠B=β,
∴∠P=![]() (β+2α);
(β+2α);
(4)∵∠B+∠A=∠1,∠C+∠D=∠2,
∴∠A+∠B+∠C+∠D=∠1+∠2,
∵∠1+∠2+∠F+∠E=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.


科目:初中数学 来源: 题型:
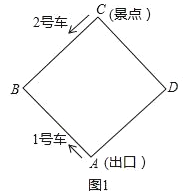
【题目】如图,某景区内的环形路是边长为1200米的正方形ABCD,现有1号、2号两辆游览车分别从出口A和景点C同时出发,1号车沿A→B→C→D→A路线、2号车沿C→B→A→D→C路线连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为300米/分.
(1)如图1,设行驶时间为t分(0≤t≤8)
①1号车、2号车离出口A的路程分别为_____米,_____米;(用含t的代数式表示)
②当两车相距的路程是600米时,求t的值;
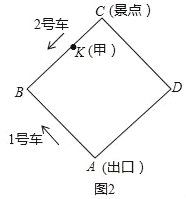
(2)如图2,游客甲在BC上的一点K(不与点B、C重合)处候车,准备乘车到出口A,设CK=x米.
情况一:若他刚好错过2号车,则他等候并搭乘即将到来的1号车;
情况二:若他刚好错过1号车,则他等候并搭乘即将到来的2号车.
请判断游客甲在哪种情况下乘车到出口A用时较多?(含候车时间)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各问题中,两个变量之间的关系不是反比例函数的是( )
A. 小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系。
B. 菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系。
C. 一个玻璃容器的体积为30L时,所盛液体的质量m与所盛液体的密度![]() 之间的关系。
之间的关系。
D. 压力为600N时,压强p与受力面积S之间的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红学习了用图形面积研究整式乘法的方法后,分别进行了如下数学探究:把一根铁丝截成两段,
探究1:小明截成了两根长度不同的铁丝,并用两根不同长度的铁丝分别围成两个正方形,已知两正方形的边长和为20cm,它们的面积的差为40cm2,则这两个正方形的边长差为________;
探究2:小红截成了两根长度相同的铁丝,并用两根同样长的铁丝分别围成一个长方形与一个正方形,若长方形的长为xcm,宽为ycm.
(1)用含x,y的代数式表示正方形的边长为________;
(2)设长方形的长大于宽,比较正方形与长方形面积哪个大,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.求证:△ABE≌△DBC.
接着张老师又让学生分小组进行探究:你还能得出什么结论?
精英小组探究的结论是:AM=DN
奋斗小组探究的结论是:△EMB≌△CNB.
创新小组探究的结论是:MN∥AC.
(1)你认为哪一小组探究的结论是正确的?
(2)选择其中你认为正确的一种情形加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边上的中线,点D,E分别在边AC和BC上,DB=DE,DE与BM相交于点N,EF⊥AC于点F,以下结论:
①∠DBM=∠CDE;②S△BDE<S四边形BMFE;③CD·EN=BN·BD;④AC=2DF.
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”,“08”和“北京”的字块,如果婴儿能够排成“2008北京”或者“北京2008”.则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com