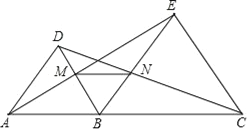
【题目】在学习了全等三角形和等边三角形的知识后，张老师出了如下一道题：如图，点B是线段AC上任意一点，分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE，连接CD、AE分别与BE和DB交于点N、M，连接MN．求证：△ABE≌△DBC．

接着张老师又让学生分小组进行探究：你还能得出什么结论？

精英小组探究的结论是：AM=DN

奋斗小组探究的结论是：△EMB≌△CNB．

创新小组探究的结论是：MN∥AC．

（1）你认为哪一小组探究的结论是正确的？

（2）选择其中你认为正确的一种情形加以证明．

参考答案：

【答案】（1）三个小组探究的结论都正确；（2）见解析

【解析】试题分析：由△ABD和△BCE是等边三角形，根据SAS易证得△ABE≌△DBC，由△ABE≌△DBC，可得∠EAC=∠NDB，又由∠ABD=∠MBN=60°，利用ASA，可证得△ABM≌△DBN，△EMB≌△CNB，又可证得△BMN是等边三角形，于是得到结论．

试题解析：（1）三个小组探究的结论都正确；

（2）∵△ABD和△BCE是等边三角形，

∴AB=BD，BC=BE，∠ABD=∠CBE=60°，

∴∠ABE=∠DBC，

在△BAE与△DBC中， ,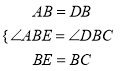

∴△ABE≌△DBC，

∴∠BAM=∠BDN，∠AEB=∠DCB，

在△ABM与△DBN中， ，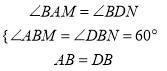

∴△ABM≌△DBN，

∴AM=DN，BM=BN，

∵∠MBN=180°﹣60°﹣60°=60°，

∴△BMN是等边三角形，

∴∠BMN=60°，

∴∠BMN=∠ABM，

∴NM∥AC，

在△EMB与△CNB中， ，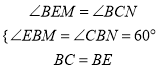

∴△EMB≌△CNB．

关闭