
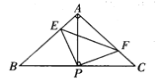
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE、PF分别交AB、AC于点E、F.给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③ 2S四边形AEPF=S△ABC;④EF=PC.上述结论正确的有 ( ).
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
证明△AEP≌△CFP,从而得到①,证明△APF≌△BPE,继而判定△EPF是等腰直角三角形,从而得到②,根据S四边形AEPF=S△AEP+S△APF,经过推导得出③,只有当EF是中位线时EF=CP才成立,从而判断④不一定正确,据此即可得答案.
∵在△ABC中,AB=AC,∠BAC=90°,P是BC中点,
∴AP=PC=PB,∠B=∠C=∠BAP=∠CAP=45°,AP⊥BC,
∴∠APB=∠APC=90°,
∵∠EPF=90°,
∴∠APE=∠CPF=90°-∠APF,
在△AEP和△CFP中,
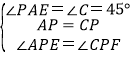 ,
,
∴△AEP≌△CFP,
同理△APF≌△BPE,
∴AE=CF,PE=PF,
∴△EPF是等腰直角三角形,
∴S△AEP=S△CPF,
∴S四边形AEPF=S△AEP+S△APF,
=S△CPF+S△APF,
=S△APC,
=![]() S△ABC,
S△ABC,
即2S四边形AEPF=S△ABC;
只有当EF为中位线时才有EF=CP,其余情况下都不相等,
∴①②③正确,④错误,
即正确的有3个,
故选C.


科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
 已知:两条线段a、b.
已知:两条线段a、b.
求作:菱形AMBN,使得其对角线分别等于b和2a.
尺规作图:作对角线等于已知线段的菱形.
 已知:两条线段a、b.
已知:两条线段a、b.
求作:菱形AMBN,使得其对角线分别等于b和2a.
小军的作法如下:
如图
(1)画一条线段AB等于b;
(2)分别以A、B为圆心,大于![]() AB的长为半径,
AB的长为半径,
在线段AB的上下各作两条弧,两弧相交于P、Q两点;
(3)作直线PQ交AB于O点;
(4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.
如图
(1)画一条线段AB等于b;
(2)分别以A、B为圆心,大于![]() AB的长为半径,
AB的长为半径,
在线段AB的上下各作两条弧,两弧相交于P、Q两点;
(3)作直线PQ交AB于O点;
(4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.
老师说:“小军的作法正确.”
该上面尺规作图作出菱形AMBN的依据是_______________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.
已知:如图,钝角∠AOB.
求作:∠AOB的角平分线.
作法:
①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于![]() DE的长为半径作弧,在∠AOB内,两弧交于点C;
DE的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
请回答:该尺规作图的依据是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2017OB2017.则点B2017的坐标是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料:
材料一:我们可以将任意三位数记为![]() (其中a,b,c分别表示该数百位数字、十位数字和个位数字,且a≠0),显然
(其中a,b,c分别表示该数百位数字、十位数字和个位数字,且a≠0),显然![]() =100a+10b+c.
=100a+10b+c.
材料二:若一个三位数的百位数字、十位数字和个位数字均不为0,则称之为原始数,比如123就是一个原始数,将原始数的三个数位上的数字交换顺序,可产生出5个原始数,比如由123可以产生出132,213,231,312,321这5个原始数.将这6个数相加,得到的和1332称为由原始数123生成的终止数.利用材料解决下列问题:
(1)分别求出由下列两个原始数生成的终止数:243,537;
(2)若一个原始数![]() 的终止数是另一个原始数
的终止数是另一个原始数![]() 的终止数的3倍,分别求出所有满足条件的这两个原始数.
的终止数的3倍,分别求出所有满足条件的这两个原始数.
查看答案和解析>>
科目:初中数学 来源: 题型:
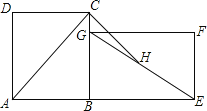
【题目】如图,在长方形ABCD中,AC是对角线.将长方形ABCD绕点B顺时针旋转90°到长方形GBEF位置,H是EG的中点.若AB=6,BC=8,则线段CH的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F. 
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com