
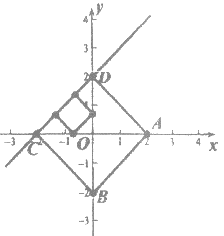
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.例如:如图l,正方形ABCD是一次函数![]() 图象的其中一个伴侣正方形.
图象的其中一个伴侣正方形.
(1)若某函数是一次函数![]() ,直接写出它的图象的所有伴侣正方形的边长;
,直接写出它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数![]() (k>0),它的图象的伴侣正方形为ABCD,点D(3,m)(m<3)在这个反比例函数图象上,求m的值及反比例函数解析式;
(k>0),它的图象的伴侣正方形为ABCD,点D(3,m)(m<3)在这个反比例函数图象上,求m的值及反比例函数解析式;
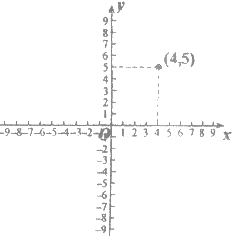
(3)若某函数是二次函数![]() (a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(4,5).直接写出所有伴侣正方形在抛物线上的另一个顶点坐标及相应的抛物线解析式.
(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(4,5).直接写出所有伴侣正方形在抛物线上的另一个顶点坐标及相应的抛物线解析式.
【答案】(1)![]() 或2
或2![]() ;(2)m的值为
;(2)m的值为![]() ,反比例函数解析式为
,反比例函数解析式为![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)先正确地画出图形,再利用正方形的性质确定相关点的坐标从而计算正方形的边长,注意思维的严密性.
(2)因为ABCD为正方形,所以可作垂线得到等腰直角三角形,利用点D(2,m)的坐标表示出点C的坐标从而求解.
(3)注意思维的严密性,抛物线开口既可能向上,也可能向下.当抛物线开口向上时,正方形的另一个顶点也是在抛物线上,这个点既可能在点(4,5)的左边,也可能在点(4,5)的右边,过点(4,5)向x轴作垂线,利用全等三角形确定线段的长即可确定抛物线上另一个点的坐标;当抛物线开口向下时也是一样地分为两种情况来讨论.
(1)(I)当点A在x轴正半轴、点B在y轴负半轴上时:
正方形ABCD的边长为![]() .
.
(II)当点A在x轴负半轴、点B在y轴正半轴上时:
设正方形边长为a,易得![]()
解得a=![]() ,此时正方形的边长为
,此时正方形的边长为![]() .
.
∴所求“伴侣正方形”的边长为![]() 或
或![]() ;
;
(2)如图,作DE⊥x轴,CF⊥y轴,垂足分别为点E.F,
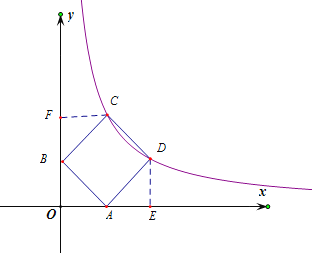
易证△ADE≌△BAO≌△CBF.
∵点D的坐标为(3,m),m<3,
∴DE=OA=BF=m,
∴OB=AE=CF=3m.
∴OF=BF+OB=3,
∴点C的坐标为(3m,3).
∴3m=3(3m),解得m=![]() .
.
∴反比例函数的解析式为![]() .
.
(3)另一个顶点坐标为(9,-4),抛物线解析式为![]() ;
;
另一个顶点坐标为(-l,4),抛物线解析式为![]() ;
;
另一个顶点坐标为(-5,9),抛物线解析式为![]() ;
;
另一个顶点坐标为(5,1),抛物线解析式为![]() .
.


科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
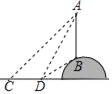
【题目】如图,为了测量小山顶的铁塔AB高度,王华和杨丽在平地上的C点处测得A点的仰角为45°,向前走了18m后到达D点,测得A点的仰角为60°,B点的仰角为30°
(1)求证:AB=BD;
(2)求证铁塔AB的高度.(结果精确到0.1米,其中![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
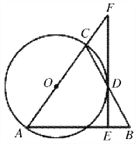
【题目】如图,在△ABC中,AB=AC,以AC为直径作![]() 交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证: EF与![]() 相切;
相切;
(2)若AE=6,![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
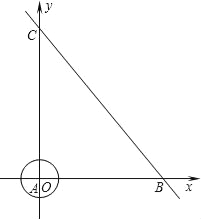
【题目】如图,在直角坐标系中,半径为1的⊙A圆心与原点O重合,直线l分别交x轴、y轴于点B、C,点B的坐标为(6,0),∠ABC=60°.
(1)若点P是⊙A上的动点,则P到直线BC的最小距离是 .
(2)若点A从原点O出发,以1个单位/秒的速度沿着线路OB→BC→CO运动,回到点O停止运动,⊙A随着点A的运动而移动.设点A运动的时间为t.
①求⊙A在整个运动过程中与坐标轴相切时t的取值;
②求⊙A在整个运动过程中所扫过的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在矩形ABCD中,AB=3,AD=4,点P为AB边上的动点(P与A、B不重合),将△BCP沿CP翻折,点B的对应点B1在矩形外,PB1交AD于E,CB1交AD于点F.
(1)如图1,求证:△APE∽△DFC;
(2)如图1,如果EF=PE,求BP的长;
(3)如图2,连接BB′交AD于点Q,EQ:QF=8:5,求tan∠PCB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
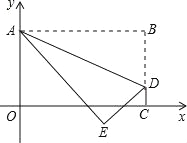
【题目】将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,当△ADE是等腰直角三角形时,点E的坐标为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com