
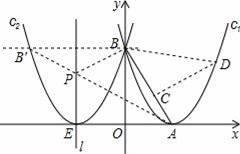
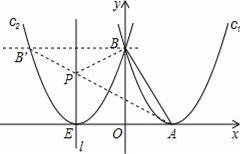
已知,如图所示,抛物线c1:y=ax2+bx+c的顶点A在x轴的正半轴上,并与y轴交于点B,OA=
 ,AB=
,AB=
 ,抛物线c2与抛物线c1关于y轴对称.
,抛物线c2与抛物线c1关于y轴对称.
(1)求抛物线c1的函数解析式,并直接写出抛物线c2的函数解析式;
(2)设l是抛物线c2的对称轴,P是l上的一点,求当△PAB的周长最小时点P的坐标;
(3)在抛物线c1上是否存在点D,过点D作DC⊥AB于C,使得△DCB与△AOB相似?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.


【考点】二次函数综合题.
【专题】综合题.
【分析】(1)在Rt△OAB中OA=
 ,AB=
,AB=
 ,求得OB的长,从而根据OA,OB得到点A,D坐标,点A坐标即为其顶点坐标,从而得到C1,C2C1关于原点对称,从而得到C2的顶点坐标,即其对称轴,从而得到C2解析式.
,求得OB的长,从而根据OA,OB得到点A,D坐标,点A坐标即为其顶点坐标,从而得到C1,C2C1关于原点对称,从而得到C2的顶点坐标,即其对称轴,从而得到C2解析式.
(2)作BB′∥x轴交C2于点B′则点B′即为点B关于l的对称点,连接AB′交l于点P即为所求点.先求得直线AB′,代入对称轴l的x值,从而进一步求得点P.
(3)设点设点D(x,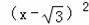
 ),求得BD,求得直线AB,求得点D到直线AB的距离,若△DCB与△AOB相似,则
),求得BD,求得直线AB,求得点D到直线AB的距离,若△DCB与△AOB相似,则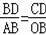
 或
或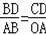
 ,代入求得的等式是否是否符合,符合则点D存在.
,代入求得的等式是否是否符合,符合则点D存在.
【解答】解:(1)∵在Rt△OAB中OA=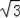
 ,AB=
,AB=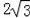
 ,
,
∴OB=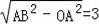
 ,
,
∴点A(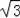
 ,0),点B(0,3).
,0),点B(0,3).
则由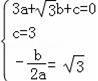
 ,
,
解得:a=1,b=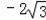
 ,c=3,
,c=3,
∴C1的解析式为:y=x2﹣2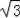
 x+3=
x+3=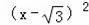
 .
.
则点A关于y轴的对称点为(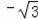
 ,0),
,0),
相当于C1向左平移了2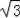
 个单位,
个单位,
∴C2的解析式为: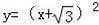
 ;
;
(2)作BB′∥x轴交C2于点B′则点B′即为点B关于l的对称点,连接AB′交l于点P即为所求点.
此时AB′即为△APB所形成三角形的最小周长.两点之间线段最短.
∵点A(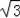
 ,0),点B(0,3),
,0),点B(0,3),
∴E(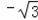
 ,0),
,0),
∴B′(﹣2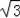
 ,3),
,3),
则设直线AB′为y=kx+b,代入A,B′得: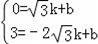
 .
.
解得:k=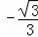
 ,b=1,
,b=1,
∴直线AB′解析式为:y=
 ,
,
代入对称轴x=﹣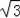
 ,则y=2,
,则y=2,
∴点P(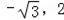
 );
);
(3)如图:存在,
知道点A,B设直线AB为y=mx+n,
代入解得:y=﹣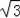
 x+3,即y+
x+3,即y+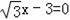
 ,
,
设点D(x,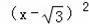
 ),则BD=
),则BD=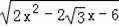
 ,
,
则点D到直线的距离CD.
知道OA=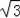
 ,OB=3,AB=2
,OB=3,AB=2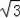
 ,
,
若△DCB与△AOB相似,则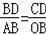
 或
或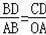
 ,
,
代入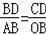
 ,
,
则点D(1,4﹣2
 ),
),
检验点D符合,
代入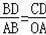
 ,
,
则点D(3,12﹣6
 ),
),
检验符合,
∴点D(1,4﹣2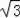
 )或(3,12﹣6
)或(3,12﹣6
 ).
).


【点评】本题考查了二次函数的综合运用,涉及到知道抛物线上的点求其解析式,求抛物线的对称轴,以及抛物线的平移.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系xOy中,已知点A的坐标为(3,a)(其中a>4),射线OA与反比例函数y=
 的图象交于点P,点B、C分别在函数y=
的图象交于点P,点B、C分别在函数y=
 的图象上,且AB∥x轴,AC∥y 轴;
的图象上,且AB∥x轴,AC∥y 轴;
(1)当点P横坐标为2,求直线AO的表达式;
(2)连接CO,当AC=CO时,求点A坐标;
(3)连接BP、CP,试猜想:
 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出
 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( )


A.7m B.8m C.9m D.10m
查看答案和解析>>
科目:初中数学 来源: 题型:
小明同学在学习了全 等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个锐角的平分线.如图:一把
等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个锐角的平分线.如图:一把 直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”你认为小明的想法正确吗?请说明理
直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”你认为小明的想法正确吗?请说明理 由.
由.

查看答案和解析>>
科目:初中数学 来源: 题型:
长方形相邻两边长分别为x、y,面积为30,则用含x的式子表示y为__________,则这个问题中,____________常量;____________是变量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com