
����Ŀ�������M��N�������Ϸֱ��ʾʵ��m,n,��������M,N����֮��ľ����ʾΪMN=m-n(m��n)��n-m(m��n)���m-n���������ν��˼�����������⣺
��֪�����ϵ�A���B�ľ���Ϊ16����λ���ȣ���A��ԭ�����࣬��ԭ��ľ���Ϊ26����λ���ȣ���B�ڵ�A���Ҳ࣬��C��ʾ�������B��ʾ������Ϊ�෴��������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������ƶ�ʱ��Ϊt�룮![]()
��1����A��ʾ����Ϊ �� ��B��ʾ����Ϊ �� ��C��ʾ����Ϊ ��
��2���ú�t�Ĵ���ʽ��ʾP����A�͵�C�ľ��룺 PA= �� PC= ��
��3������P�˶���B��ʱ����Q��A���������ÿ��3����λ���ٶ���C���˶��� Q�㵽��C�����������ͬ�����ٶȷ��أ��˶����յ�A��
���ڵ�Q���C�˶������У��ܷ��ϵ�P?���ܣ��������Q�˶������ϣ�
���ڵ�Q��ʼ�˶���P��Q����֮��ľ����ܷ�Ϊ2����λ������ܣ��������ʱ��P��ʾ������������ܣ���˵�����ɣ�
���𰸡�
��1���⣺-26��-10��10
��2���⣺t��36-t
��3���⣺���ڵ�Q���C�˶������У����Q�˶�x���ϵ�P�����������
3x=x+16��
���x=8��
���ڵ�Q���C�˶������У����ϵ�P����Q�˶�8���ϣ�
�ڷ����������
����Q��A�����C�˶�ʱ��
�����Q�ڵ�P�ĺ��棬��ô1x+16-3x=2�����x=7����ʱ��P��ʾ������-3��
�����Q�ڵ�P��ǰ�棬��ô3x-��1x+16��=2�����x=9����ʱ��P��ʾ������-1��
����Q��C�㷵�ص���Aʱ��
�����Q�ڵ�P�ĺ��棬��ô3x+1x+16+2=2��36�����x= ![]() ����ʱ��P��ʾ������
����ʱ��P��ʾ������ ![]() ��
��
�����Q�ڵ�P��ǰ�棬��ô3x+1x+16=2��36+2�����x= ![]() ����ʱ��P��ʾ������
����ʱ��P��ʾ������ ![]() ��
��
���ڵ�Q��ʼ�˶���P��Q����֮��ľ�����Ϊ2����λ����ʱ��P��ʾ�����ֱ���-3��-1�� ![]() ��
�� ![]() ��
��
����������1���ߵ�A��ԭ�����࣬��ԭ��ľ���Ϊ26����λ���ȣ�
���A��ʾ����Ϊ-26��
�ߵ�A���B�ľ���Ϊ16����λ���ȣ��ҵ�B�ڵ�A���Ҳ࣬
���B��ʾ����Ϊ-26+16=-10��
�ߵ�C��ʾ�������B��ʾ������Ϊ�෴����
���C��ʾ����Ϊ10.
�� 2 ��PA=1��t=t��
PC=AC-PA=36-t.
��1���ɵ�A��ԭ�����࣬��ԭ��ľ���Ϊ26����λ���ȣ���֪��A��ʾ����Ϊ-26�����ݵ�B�ڵ�A���Ҳ࣬��A���B�ľ���Ϊ16����λ���ȣ��ó���B��ʾ����Ϊ-10���ɵ�C��ʾ�������B��ʾ������Ϊ�෴�����õ���C��ʾ����Ϊ10��
��2������·��=�ٶȡ�ʱ�䣬�ɵ�PA=1��t=t����PC=AC-PA�ɵ�PC=36-t��
��3�����ڵ�Q���C�˶������У����Q�˶�x���ϵ�P�����ݵ�Q�ϵ�Pʱ����Q�˶���·��=��P�˶���·�̣��г����̣��ⷽ�̼��ɣ�
�ڷ������������Q��A�����C�˶�ʱ���ֵַ�Q�ڵ�P�ĺ������Q�ڵ�P��ǰ�棻��Q��C�㷵�ص���Aʱ���ֵַ�Q�ڵ�P�ĺ������Q�ڵ�P��ǰ�棬���㼴�ɵó��𰸡�


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������O��ֱ��Ϊ6cm��OA="5" cm����ô��A����O��λ�ù�ϵ�ǣ� ��
A.��A��Բ��B.��A��Բ��C.��A��Բ��D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͬ�������ظ����飬���¼�A�����ĸ�����![]() �� ���г����У���ȷ���ǣ�������
�� ���г����У���ȷ���ǣ�������
A.�¼�A������Ƶ����![]()
B.�����������������飬�¼�Aֻ������7��
C.��100���������飬�¼�Aһ������7��
D.��100���������飬�¼�A���ܷ���7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�k��1��x2��4x+4��0��ʵ������ע���˴���δ˵���˷���ΪһԪ���η��̣�Ӧ�ֱ���k��1��k��1�����Σ�����k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���P��x��y���ĺ�����x�ľ���ֵ��ʾΪ|x|��������y�ľ���ֵ��ʾΪ|y|�����ǰѵ�P��x��y���ĺ�������������ľ���ֵ֮�ͽ�����P��x��y���Ĺ���ֵ����Ϊ��P��������P��=![]() +
+![]() �������еġ�+�������������еļӷ���
�������еġ�+�������������еļӷ���
��1�����A����1��3����B��![]() ��
��![]() ���Ĺ���ֵ��A������B����
���Ĺ���ֵ��A������B����
��2����M�ڷ���������![]() ��ͼ���ϣ��ҡ�M��=4�����M�����ꣻ
��ͼ���ϣ��ҡ�M��=4�����M�����ꣻ
��3��������������N��=3�����е�NΧ�ɵ�ͼ�ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�ڡ�AOB���ڲ�����M��N�ֱ��ǵ�P����ֱ��OA��OB�ĶԳƵ㣬�߶�MN��OA��OB�ڵ�E��F������PEF���ܳ���30cm�����߶�MN�ij��� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OB�ǡ�AOC��ƽ���ߣ�OD�ǡ�EOC��ƽ����.
��1�������AOD=75�㣬��BOC=19�㣬���DOE�Ķ�����
��2�������BOD=56�㣬���AOE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����E��AC�ϣ���F��AB�ϣ�BE��CF���ڵ�O���ҡ�C=2��B����BFC�ȡ�BEC��20�㣬���C�Ķ����� 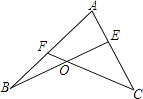
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ� ��
A.һ���������ľ���ֵ��С��������
B.�������������ľ���ֵ��ȣ��������������
C.�������������ľ���ֵ��ȣ�������������Ϊ�෴��
D.��a�ľ���ֵ����a
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com