如图，AB∥DC，请你添加一个条件使得△ABD≌△CDB，可添条件是__________．（添一个即可）
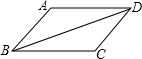
AB=CD等（答案不唯一）．
【考点】全等三角形的判定．
【专题】开放型．
【分析】由已知二线平行，得到一对角对应相等，图形中又有公共边，具备了一组边和一组角对应相等，还缺少边或角对应相等的条件，结合判定方法及图形进行选择即可．
【解答】解：∵AB∥DC，
∴∠ABD=∠CDB，又BD=BD，
①若添加AB=CD，利用SAS可证两三角形全等；
②若添加AD∥BC，利用ASA可证两三角形全等．（答案不唯一）
故填AB=CD等（答案不唯一）
【点评】本题考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关健．
科目：初中数学 来源： 题型：
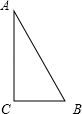
如图，△ABC中，∠C=Rt∠，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．
（1）出发2秒后，求△ABP的周长．
（2）问t为何值时，△BCP为等腰三角形？
（3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？
查看答案和解析>>
科目：初中数学 来源： 题型：
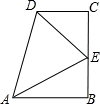
在数学活动课上，小明提出这样一个问题：∠B=∠C=90°，E是BC的中点，DE平分∠ADC，如图，则下列说法正确的有几个，大家一起热烈地讨论交流，小英第一个得出正确答案，是( )
（1）AE平分∠DAB；
（2）△EBA≌△DCE；
（3）AB+CD=AD；
（4）AE⊥DE；
（5）AB∥CD．
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目：初中数学 来源： 题型：
如图：E在△ABC的AC边的延长线上，D点在AB边上，DE交BC于点F，DF=EF，BD=CE，过D作DG∥AC交BC于G．求证：
（1）△GDF≌△CEF；
（2）△ABC是等腰三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
课本等腰三角形的轴对称性一节，我们最后通过直角三角形纸片折叠发现了定理“直角三角形斜边上的中线等于斜边的一半”．
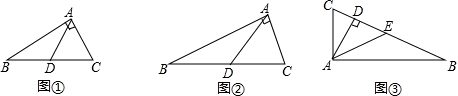
（1）小聪同学画出了如图①所示的一个特殊的直角三角形，其中∠BAC为直角，AD为斜边BC上的中线，∠B=30°．它证明上面定理思路如下：延长AD至点E，使DE=AD
，连结BE，再证△ABC≌△BAE，你认为小聪能否完成证明？__________（只需要填“能”或“不能”）；
（2）小聪同学还想借助图②，任意的Rt△ABC为直角，AD为斜边BC上的中线，证明或推翻结论AD=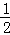
BC，请你帮助小聪同学
完成；
（3）如图③，在△ABC中AD⊥BC，垂足为D，如果CD=1，AD=2，BD=4，求△ABC的中线AE的长度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
