
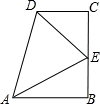
在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个,大家一起热烈地讨论交流,小英第一个得出正确答案,是( )
(1)AE平分∠DAB;
(2)△EBA≌△DCE;
(3)AB+CD=AD;
(4)AE⊥DE;
(5)AB∥CD.
A.1个 B.2个 C.3个 D.4个
D
【考点】全等三角形的判定与性质;平行线的性质.
【分析】此题可以通过作辅助线来得解,取AD的中点F,连接EF.根据平行线的性质可证得(1)(4)(5),根据梯形中位线定理可证得(3)正确.根据全等三角形全等的判定可证得(2)的正误,即可得解.
【解答】解:如图:取AD的中点F,连接EF.
∵∠B=∠C=90°,
∴AB∥CD;[结论(5)]
∵E是BC的中点,F是AD的中点,
∴EF∥AB∥CD,2EF=AB+CD(梯形中位线定理)①;
∴∠CDE=∠DEF(两直线平等,内错角相等),
∵DE平分∠ADC,
∴∠CDE=∠FDE=∠DEF,
∴DF=EF;
∵F是AD的中点,∴DF=AF,
∴AF=DF=EF②,
由①得AF+DF=AB+CD,即AD=AB+CD;[结论(3)]
由②得∠FAE=∠FEA,
由AB∥EF可得∠EAB=∠FEA,
∴∠FAE=∠EAB,即EA平分∠DAB;[结论(1)]
由结论(1)和DE平分∠ADC,且DC∥AB,可得∠EDA+∠DAE=90°,则∠DEA=90°,即AE⊥DE;[结论(4)].
由以上结论及三角形全等的判定方法, 无法证明△EBA≌△DCE.
无法证明△EBA≌△DCE.
正确的结论有4个,故选D.

【点评】本题考查了平行线的判定及性质、梯形中位线定理、等腰三角形的性质、全等三角形的判定等知识点,是一道难度较大的综合题型.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:初中数学 来源: 题型:
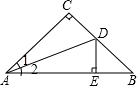
如图,在△ABC中,∠C=90°,AC=BC,AD是∠CAB的角平分线,DE⊥AB于点E,若AB=6cm,则△DEB的周长是( )
A.5cm B.6cm C.7cm D.8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
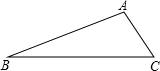
如图,已知△ABC,AC<AB.
(1)用直尺和圆规作出一条过点A的直线l,使得点C关于直线l的对称点落在边AB上(不写作法,保留作图痕迹);
(2)设直线l与边BC的交点为D,且∠C=2∠B,请你通过观察或测量,猜想线段AB、AC、CD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
在下列各组条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC= EF,AC=DF
EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
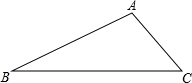
如图,在△ABC中,∠B=30°,∠C=45°,AC=2,点P是△ABC三条边上的任意一点.若△ACP为等腰三角形,在图中作出所有符合条件的点P,要求:
①尺规作图,不写作法,保留痕迹;
②若符合条件的点P不只一个,请标注P1、P2…
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )

A.118° B.119° C.120° D.121°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com