
在下列各组条件中,不能说明△ABC≌△DEF的是( )
A.AB=DE,∠B=∠E,∠C=∠F B.AC=DF,BC=EF,∠A=∠D
C.AB=DE,∠A=∠D,∠B=∠E D.AB=DE,BC= EF,AC=DF
EF,AC=DF
B【考点】全等三角形的判定.
【分析】根据题目所给的条件结合判定三角形全等的判定定理分别进行分析即可.
【解答】解:A、AB=DE,∠B=∠E,∠C=∠F,可以利用AAS定理证明△ABC≌△DEF,故此选项不合题意;
B、AC=DF,BC=EF,∠A=∠D不能证明△ABC≌△DEF,故此选项符合题意;
C、AB=DE,∠A=∠D,∠B=∠E,可以利用ASA定理证明△ABC≌△DEF,故此选项不合题意;
D、AB=DE,BC=EF,AC=DF可以利用SSS定理证明△ABC≌△DEF,故此选项不合题意;
故选:B.
【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠C=90°,∠B=30°,CD是斜边AB上的高,AD=3cm,则AB的长度是( )
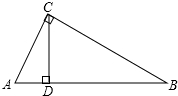
A.3cm B.6cm C.9cm D.12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
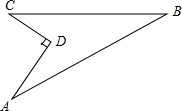
查看答案和解析>>
科目:初中数学 来源: 题型:
在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个,大家一起热烈地讨论交流,小英第一个得出正确答案,是( )
(1)AE平分∠DAB;
(2)△EBA≌△DCE;
(3)AB+CD=AD;
(4)AE⊥DE;
(5)AB∥CD.
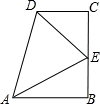
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )

A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com