练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，∠C=90°，AC=BC，AD是∠CAB的角平分线，DE⊥AB于点E，若AB=6cm，则△DEB的周长是(     )

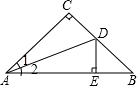
    A．5cm  B．6cm  C．7cm  D．8cm


    B【考点】角平分线的性质；等腰直角三角形．

    【分析】根据角平分线的性质得到DC=DE，AC=AE，根据三角形的周长公式计算即可．

    【解答】解：∵AD是∠CAB的角平分线，DE⊥AB，∠C=90°，

    ∴DC=DE，AC=AE，

    ∴△DEB的周长=DE+BE+BD=BE+DC+BD=BE+BC=BE+AE=AB=6cm．

    故选：B．

    【点评】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，∠A=36°，∠DBC=36°，∠C=72°，则图中等腰三角形有__________个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下面有4个汽车标志图案，其中是轴对称图形的有(     )

    A．1个  B．2个   C．3个  D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （1）如图（1），在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．

    ①求证：BE+CF＞EF．

    ②若∠A=90°，探索线段BE、CF、EF之间的数量关系，并加以证明；

    （2）如图（2），在四边形ABCD中，∠B+∠C=180°，DB=DC，∠BDC=120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC与△ADC中，已知AD=AB，在不添加任何辅助线的前提下，要使△ABC≌△ADC，只需再添加的一个条件可以是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，点O是△ABC内一点且到△ABC三边的距离相等，∠A=40°，则∠BOC=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在数学活动课上，小明提出这样一个问题：∠B=∠C=90°，E是BC的中点，DE平分∠ADC，如图，则下列说法正确的有几个，大家一起热烈地讨论交流，小英第一个得出正确答案，是(     )

    （1）AE平分∠DAB；

    （2）△EBA≌△DCE；

    （3）AB+CD=AD；

    （4）AE⊥DE；

    （5）AB∥CD．

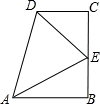
    A．1个  B．2个   C．3个  D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，△ABC中，AC=AD=BD，∠DAC=80°，则∠B的度数是(     )

    A．40°   B．35°    C．25°   D．20°

    查看答案和解析>>

    同步练习册答案