
课本等腰三角形的轴对称性一节,我们最后通过直角三角形纸片折叠发现了定理“直角三角形斜边上的中线等于斜边的一半”.
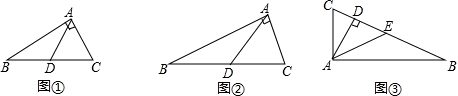
(1)小聪同学画出了如图①所示的一个特殊的直角三角形,其中∠BAC为直角,AD为斜边BC上的中线,∠B=30°.它证明上面定理思路如下:延长AD至点E,使DE=AD ,连结BE,再证△ABC≌△BAE,你认为小聪能否完成证明?__________(只需要填“能”或“不能”);
,连结BE,再证△ABC≌△BAE,你认为小聪能否完成证明?__________(只需要填“能”或“不能”);
(2)小聪同学还想借助图②,任意的Rt△ABC为直角,AD为斜边BC上的中线,证明或推翻结论AD=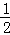 BC,请你帮助小聪同学
BC,请你帮助小聪同学 完成;
完成;
(3)如图③,在△ABC中AD⊥BC,垂足为D,如果CD=1,AD=2,BD=4,求△ABC的中线AE的长度.
【考点】全等三角形的判定与性质;勾股定理;勾股定理的逆定理.
【分析】(1)如图①所示.由三角形内角和定理可求得∠ACB=60°.然后证明△ACD≌△EBD,从而得到∠EBD=∠ACD=60°,BE=AC,∠ABE=90°然后再证明Rt△ABE≌Rt△BAC,于是得到BC=AE故此BC=2AD;
(2)如图②所示:延 长AD至点E使DE=AD,连结BE,先证明△ACD≌△EBD,得到∠C=∠EBD,从而可证明∠BAC=∠ABE,然后证明△ABC≌△BAE,从而得到AE=BC,故此BC=AE=2AD;
长AD至点E使DE=AD,连结BE,先证明△ACD≌△EBD,得到∠C=∠EBD,从而可证明∠BAC=∠ABE,然后证明△ABC≌△BAE,从而得到AE=BC,故此BC=AE=2AD;
(3)根据勾股定理得:AC2=5,AB2=20,于是可得到AC2+AB2=BC2.于是得到△ABC是直角三角形,根据结论可知△ABC的中线AE的长度= BC=
BC=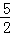 .
.
【解答】解:(1)能.
理由:如图①所示.
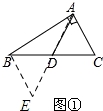
∵∠BAC=90°,∠ABC=30°,
∴∠ACB=60°.
在△ACD和△EBD中,

∴△ACD≌△EBD.
∴∠EBD=∠ACD=60° ,BE=AC.
,BE=AC.
∴∠ABE=90°.
在Rt△ABE和Rt△BAC中,
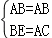 ,
,
∴Rt△ABE≌Rt△BAC.
∴BC=AE.
∴BC=2AD.
∴AD=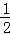 BC.
BC.
(2)证明:如图②所示:延长AD至点E使DE=AD,连结BE.
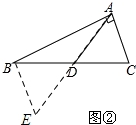
在△ACD和△EBD中,
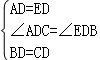 ,
,
∴△ACD≌△EBD.
∴∠C=∠EBD
∴∠C+∠ABC=∠ABC+∠EBD,即∠BAC=∠ABE.
在△ABC和△BAE中,
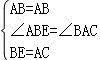 ,
,
∴△ABC≌△BAE.
∴AE=BC.
∴BC=AE=2AD
∴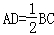 .
.
(3)∵AD⊥BC,
∴∠ADC=∠ADB=90°.
∵CD=1,AD=2,BD=4,
∴根据勾股定理得:AC2=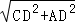 =5,AB2=
=5,AB2=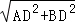 =20.
=20.
∵AC2=5,AB2=20,BC2=(1+4)2=25,
∴AC2+AB2=BC2.
∴△ABC是直角三角形.
∴△ABC的中线AE的长度=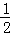 BC=
BC=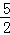 .
.
【点评】本题主要考查的是全等三角形的性质和判定的应用、勾股定理和勾股定理的逆定理的应用,根据△ACD≌△EBD、△ABC≌△BAE是解题的关键.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
在Rt△ABC中,∠ACB=90°,AC=24cm,AB=26cm,则其直角边BC的长为( )
A.6cm B.100cm C.15cm D.10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
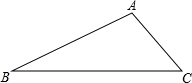
如图,在△ABC中,∠B=30°,∠C=45°,AC=2,点P是△ABC三条边上的任意一点.若△ACP为等腰三角形,在图中作出所有符合条件的点P,要求:
①尺规作图,不写作法,保留痕迹;
②若符合条件的点P不只一个,请标注P1、P2…
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com