练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在△ABC中，AB=AC=20，BC=32，点D在BC上，且AD=13，求BD的长．


    【考点】勾股定理．

    【分析】过点A作AE⊥BC于E，根据等腰三角形三线合一的性质可得BE=CE=BC，再利用勾股定理列式求出AE，然后利用勾股定理列式求出DE，即可得解．

    【解答】解：如图，过点A作AE⊥BC于E，

    ∵AB=AC，

    ∴BE=CE=BC=16，

    由勾股定理得，AE===12，

    在Rt△ADE中，DE===5，

    当点D在AE左侧时（如图）BD=BE﹣DE=16﹣5=11；

    当点D在AE右侧时，BD=BE+DE=16+5=21．

    综上所述，BD的长为11或21．

    【点评】本题考查的是勾股定理，根据题意作辅助线构造出直角三角形是解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，已知MB=ND，∠MBA=∠NDC，下列哪个条件不能判定△ABM≌△CDN(     )

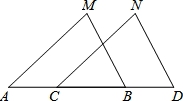
    A．∠M=∠N B．AB=CD     C．AM∥CN  D．AM=CN

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB=AC，AD=AE，∠1=∠2，求证：BD=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC≌△DEC，△ABC的周长为100cm，DE=30cm，EC=25cm，那么BC长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在下列各组条件中，不能说明△ABC≌△DEF的是(     )

    A．AB=DE，∠B=∠E，∠C=∠F      B．AC=DF，BC=EF，∠A=∠D

    C．AB=DE，∠A=∠D，∠B=∠E      D．AB=DE，BC=EF，AC=DF

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC与△ADC中，已知AD=AB，在不添加任何辅助线的前提下，要使△ABC≌△ADC，只需再添加的一个条件可以是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


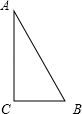
    如图，△ABC中，∠C=Rt∠，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．

    （1）出发2秒后，求△ABP的周长．

    （2）问t为何值时，△BCP为等腰三角形？

    （3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


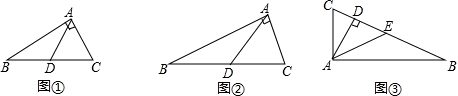
    课本等腰三角形的轴对称性一节，我们最后通过直角三角形纸片折叠发现了定理“直角三角形斜边上的中线等于斜边的一半”．

    （1）小聪同学画出了如图①所示的一个特殊的直角三角形，其中∠BAC为直角，AD为斜边BC上的中线，∠B=30°．它证明上面定理思路如下：延长AD至点E，使DE=AD，连结BE，再证△ABC≌△BAE，你认为小聪能否完成证明？__________（只需要填“能”或“不能”）；

    （2）小聪同学还想借助图②，任意的Rt△ABC为直角，AD为斜边BC上的中线，证明或推翻结论AD=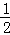BC，请你帮助小聪同学完成；

    （3）如图③，在△ABC中AD⊥BC，垂足为D，如果CD=1，AD=2，BD=4，求△ABC的中线AE的长度．

    查看答案和解析>>

    同步练习册答案