
【题目】在平面直角坐标系中,已知点P![]() ,试分别根据下列条件,求出点P的坐标:
,试分别根据下列条件,求出点P的坐标:
(1)点P在![]() 轴上;
轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P到两坐标的距离相等;
(4)点P在过A(2,-5)点,且与![]() 轴平行的直线上。
轴平行的直线上。
【答案】(1)P(0,-3);(2)P(-12,-9);(3)P(-6,-6)或(2,-2);(4)P(-4,-5).
【解析】
(1)让横坐标为0,求得m的值,代入点P的坐标即可求解;
(2)让纵坐标-横坐标=3得m的值,代入点P的坐标即可求解;
(3)根据点到两坐标轴的距离相等,横坐标与纵坐标相等或互为相反数列方程分别求出m的值,再求解即可.
(4)让纵坐标为-5求得m的值,代入点P的坐标即可求解.
解:(1)令2m+4=0,解得m=-2,
∴![]()
所以P点的坐标为(0,-3);
(2)令m-1-(2m+4)=3,解得m=-8,
∴![]()
所以P点的坐标为(-12,-9);
(3)根据题意,得2m+4=m-1或2m+4+m-1=0,
解之,得m=-5或m=-1,
∴2m+4=-6,m-1=-6或2m+4=2,m-1=-2,
∴点P的坐标为(-6,-6)或(2,-2).
(4)令m-1=-5,解得m=-4.
∴2m+4=-4,
所以P点的坐标为(-4,-5).
故答案为:(1)P(0,-3);(2)P(-12,-9);(3)P(-6,-6)或P(2,-2);(4)P(-4,-5)


科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4,AD=2,点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P、Q两点相遇时,它们同时停止运动。设Q点运动的时间为![]() (秒),在整个运动过程中,求解下面问题:
(秒),在整个运动过程中,求解下面问题:
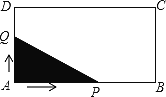
(1)当P、Q相遇时,求出![]() 的值(列方程解决问题);
的值(列方程解决问题);
(2)当△APQ的面积为![]() 时,此时t的值是_________;
时,此时t的值是_________;
(3)当△APQ为直角三角形时,直接写出相应的![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
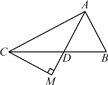
【题目】如图,在△ABC中,AD是∠BAC的平分线,且∠B=∠ADB,过点C作CM垂直于AD的延长线,垂足为M.
(1)若∠DCM=α,试用α表示∠BAD;
(2)求证:AB+AC=2AM.
查看答案和解析>>
科目:初中数学 来源: 题型:
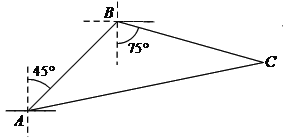
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
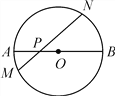
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
(3)若⊙O的半径为R,求PM2+PN2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
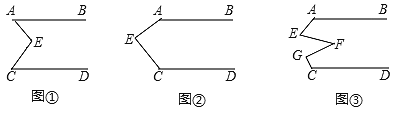
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BAE+∠DCE=∠AEC;
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠BAE+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③,若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG=______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
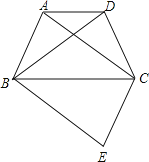
【题目】如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(1)求证:四边形ABEC是平行四边形.
(2)若AD=CD=6,∠ADC=120°,求四边形ABEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.

(1)填空:A,B两地相距 千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com