
【题目】如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
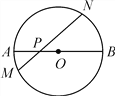
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
(3)若⊙O的半径为R,求PM2+PN2的值.
【答案】(1)MN=2![]() (2)2
(2)2![]() (3)PM2+PN2=2R2
(3)PM2+PN2=2R2
【解析】试题分析:(1)作OH⊥MN于H,连接ON,先计算出![]() ,在Rt△POH中,由于
,在Rt△POH中,由于![]() 则
则![]() 再在Rt△OHN中,利用勾股定理计算出
再在Rt△OHN中,利用勾股定理计算出![]() 然后根据垂径定理由OH⊥MN,得到HM=HN,
然后根据垂径定理由OH⊥MN,得到HM=HN,
所以![]()
(2)作OH⊥MN于H,连接ON,先计算出HM=HN=4,PH=1,在Rt△POH中,由![]() 得到OH=1,再在Rt△OHN中,利用勾股定理可计算出
得到OH=1,再在Rt△OHN中,利用勾股定理可计算出![]()
![]()
(3)作OH⊥MN于H,连接ON,根据垂定理得HM=HN,在Rt△OHN中,利用勾股定理得到![]() 在Rt△POH中,由
在Rt△POH中,由![]() 得
得![]() ,则
,则![]() 然后变形
然后变形![]() 可得到
可得到![]() 所以
所以![]() 的值为
的值为![]()
试题解析:(1)作OH⊥MN于H,连接ON,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,OP=2,
在Rt△POH中,![]()
![]()
在Rt△OHN中,![]()
![]()
∵OH⊥MN,
∴HM=HN,
![]()
(2)作OH⊥MN于H,连接ON,
则HM=HN,
∵MP=3,NP=5,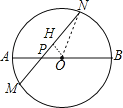
∴MN=8,
∴HM=HN=4,
∴PH=1,
在Rt△POH中, ![]()
∴OH=1,
在Rt△OHN中,∵HN=4,OH=1,
![]()
![]()
(3)作OH⊥MN于H,连接ON,
则HM=HN,
在Rt△OHN中, ![]()
在Rt△POH中, ![]()
∴OH=PH,
∴![]()
![]()


科目:初中数学 来源: 题型:
【题目】已知a、b、c是![]() 的三边,且满足
的三边,且满足![]() ,试判断
,试判断![]() 的形状.
的形状.
阅读下面解题过程:
解:由![]() 得:
得:![]() ①
①
![]() ②
②
即![]() ③
③
∴![]() 为Rt△.④
为Rt△.④
试问:以上解题过程是否正确:_________.
若不正确,请指出错在哪步?______(填代号)
错误原因是______________________.
本题的结论应为_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,![]() 表示行驶里程,
表示行驶里程,![]() (元)表示车费,请根据图象回答下列问题:
(元)表示车费,请根据图象回答下列问题:
(1)出租车的起步价是多少元;
(2)当 ![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意写出一个数位不含零的三位数,任取三个数字中的两个,组合成所有可能的两位数(有6个),求出所有这些两位数的和,然后将它除以原三位数的各个数位上的数的和.例如,对三位数223,取其两个数字组成所有可能的两位数:22,23,22,23,32,32.它们的和是154.三位数223各位数的和是7,![]() 再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.
再换几个数试一试,你发现了什么?请写出你按上面方法的探索过程和所发现的结果,并运用代数式的知识说明所发现的结果的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P![]() ,试分别根据下列条件,求出点P的坐标:
,试分别根据下列条件,求出点P的坐标:
(1)点P在![]() 轴上;
轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P到两坐标的距离相等;
(4)点P在过A(2,-5)点,且与![]() 轴平行的直线上。
轴平行的直线上。
查看答案和解析>>
科目:初中数学 来源: 题型:
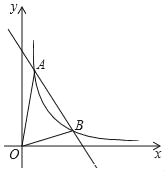
【题目】如图一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(1,6),B(n,2)两点.
(x>0)的图象交于A(1,6),B(n,2)两点.
(1)求一次函数和反比例函数的解析式
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
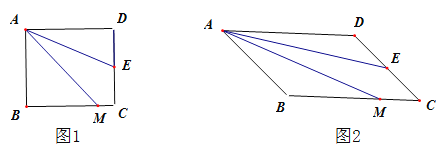
【题目】如图,四边形ABCD是矩形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)证明:AM=AD+MC.
(2)若四边形ABCD是平行四边形,其它条件不变,如图,(1)中的结论是否成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=![]() (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )
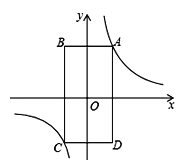
A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com