
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒. ![]()
(1)写出数轴上点B表示的数;点P表示的数(用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P,Q同时出发,问多少秒时P,Q之间的距离恰好等于2?
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速到家动,若点P,Q同时出发,问多少秒时P,Q之间的距离恰好又等于2?
(4)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请他画出图形,并求出线段MN的长.
【答案】
(1)﹣12;8﹣5t
(2)解:若点P、Q同时出发,设t秒时P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
由题意得3t+2+5t=20,解得t=2.25;
②点P、Q相遇之后,
由题意得3t﹣2+5t=20,解得t=2.75.
答:若点P、Q同时出发,2.25或2.75秒时P、Q之间的距离恰好等于2
(3)解:设点P运动x秒时,P、Q之间的距离恰好等于2.分两种情况:
①点P、Q相遇之前,
则5x﹣3x=20﹣2,
解得:x=9;
②点P、Q相遇之后,
则5x﹣3x=20+2
解得:x=11.
答:若点P、Q同时出发,9或11秒时P、Q之间的距离恰好又等于2
(4)解:线段MN的长度不发生变化,都等于10;理由如下:
① 当点P在点A、B两点之间运动时:
![]()
MN=MP+NP= ![]() AP+
AP+ ![]() BP=
BP= ![]() (AP+BP)=
(AP+BP)= ![]() AB=
AB= ![]() ×20=10,
×20=10,
②当点P运动到点B的左侧时:
![]()
MN=MP﹣NP= ![]() AP﹣
AP﹣ ![]() BP=
BP= ![]() (AP﹣BP)=
(AP﹣BP)= ![]() AB=10,
AB=10,
则线段MN的长度不发生变化,其值为10
【解析】解:(1)数轴上点B表示的数为8﹣20=﹣12;点P表示的数为8﹣5t; 所以答案是:﹣12;8﹣5t.
【考点精析】掌握数轴和两点间的距离是解答本题的根本,需要知道数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中,装有红、黄、白、黑四种只有颜色不同的小球,其中红色小球有30个,黄、白、黑色小球的数目相同.为估计袋中黄色小球的数目,每次将袋中小球搅匀后摸出一个小球记下颜色,放回后再次搅匀…多次试验发现摸到红球的频率是![]() ,则估计黄色小球的数目是 .
,则估计黄色小球的数目是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为1,A,B,C都在格点上. 
(1)过点C画直线AB的平行线(仅利用所给方格纸和直尺作图,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段的长度是点A到直线BC的距离;线段AH的长度是点H到直线的距离.
(4)线段AG、AH的大小关系为:AGAH.理由: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒. 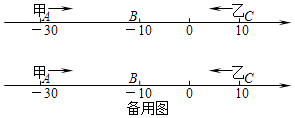
(1)甲,乙在数轴上的哪个点相遇?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A,B,C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在经典诵读活动中,对全校学生用A,B,C,D四个等级进行评价,现从中随机抽取若干个学生进行调查,绘制出了两幅不完整的统计图,如图所示,请你根据图中信息解答下列问题: 
(1)共抽取了多少个学生进行调查?
(2)分别求出B等级的人数和图乙中B等级所占圆心角的度数.
(3)将图甲中的折线统计图补充完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com