
【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒. 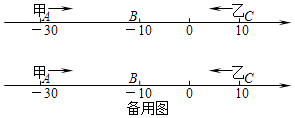
(1)甲,乙在数轴上的哪个点相遇?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A,B,C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
【答案】
(1)解:设x秒后,甲、乙在数轴上相遇.
则4x+6x=40,解得x=4,
﹣30+4×4=﹣14
答:甲,乙在数轴上表示﹣14的点相遇
(2)解:解:能.显然,当甲在点C右侧时,甲到A,B,C的距离和大于40+20=60,
故甲应运动到AB或BC之间.
设y秒后,甲到A,B,C的距离和为48个单位.
当甲在AB之间时:4y+(20﹣4y)+(40﹣4y)=48,
解得y=3;
当甲在BC之间时:4y+(4y﹣20)+(40﹣4y)=48,
解得x=7;
答:3或7秒后,甲到A,B,C的距离和为48个单位
(3)设甲调头z秒后与乙相遇.
若甲从A向右运动3秒时返回,
甲表示的数为:﹣30+4×3﹣4z;乙表示的数为:10﹣6×3﹣6z,
由题意得:﹣30+4×3﹣4z=10﹣6×3﹣6z,
解得z=5.
相遇点表示的数为:﹣30+4×3﹣4×5=﹣38.
若甲从A向右运动7秒时返回,
甲表示的数为:﹣30+4×7﹣4z;乙表示的数为:10﹣6×7﹣6z,
依据题意得:﹣30+4×7﹣4z=10﹣6×7﹣6z,
解得z=﹣15(舍去).
(注:此时甲在表示﹣2的点上,乙在表示﹣32的点上,乙在甲的左侧,甲追及不上乙,因而不可能相遇.)
答:甲从A向右运动3秒时返回,甲,乙能在数轴上相遇,相遇点表示的数为﹣38.
【解析】(1)设x秒后甲与乙相遇,根据甲与乙的路程和为40,可列出方程求解即可;(2)设y秒后甲到A,B,C三点的距离之和为48个单位,分甲应为于AB或BC之间两种情况讨论即可求解:(3)设z秒后甲与乙在数轴上相遇,需要分类讨论:①若甲从A向右运动3秒时返回;②若甲从A向右运动7秒时返回,分别表示出甲、乙表示的数,结合线段间的和差关系列出方程并解答.
【考点精析】关于本题考查的数轴,需要了解数轴是规定了原点、正方向、单位长度的一条直线才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】两个相似三角形的对应边分别是15cm和23cm,它们的周长相差40cm,则这两个三角形的周长分别是( )
A.45cm,85cm
B.60cm,100cm
C.75cm,115cm
D.85cm,125cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒. ![]()
(1)写出数轴上点B表示的数;点P表示的数(用含t的代数式表示)
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P,Q同时出发,问多少秒时P,Q之间的距离恰好等于2?
(3)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速到家动,若点P,Q同时出发,问多少秒时P,Q之间的距离恰好又等于2?
(4)若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请他画出图形,并求出线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上A、B两点所表示的数分别为﹣2和8. ![]()
(1)求线段AB的长;
(2)已知点P为数轴上点A左侧的一点,且M为PA的中点,N为PB的中点. 请你画出图形,观察MN的长度是否发生改变?若不变,求出线段MN的长;若改变,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com