
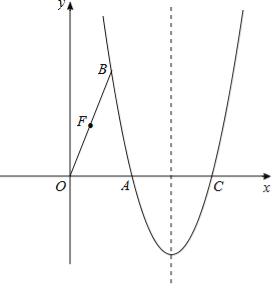
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ≈„ќпѕя![]() Њ≠єэµгA£®
Њ≠єэµгA£®![]() £ђ0£©ЇЌµгB£®1£ђ
£ђ0£©ЇЌµгB£®1£ђ![]() £©£ђ”лx÷бµƒЅн“їЄцљїµгќ™C£Ѓ
£©£ђ”лx÷бµƒЅн“їЄцљїµгќ™C£Ѓ
£®1£©«у≈„ќпѕяµƒЇѓ э±ніп љ£ї
£®2£©µгD‘Џґ‘≥∆÷бµƒ”“≤а£ђx÷б…ѕЈљµƒ≈„ќпѕя…ѕ£ђ«“°ѕBDA=°ѕDAC£ђ«уµгDµƒ„ш±к£ї
£®3£©‘Џ£®2£©µƒћхЉюѕ¬£ђЅђљ”BD£ђљї≈„ќпѕяґ‘≥∆÷б”ЏµгE£ђЅђљ”AE£Ѓ
Ґў≈–ґѕЋƒ±я–ќOAEBµƒ–ќ„і£ђ≤ҐЋµ√чјн”…£ї
ҐЏµгF «OBµƒ÷–µг£ђµгM «÷±ѕяBDµƒ“їЄцґѓµг£ђ«“µгM”лµгB≤ї÷ЎЇѕ£ђµ±°ѕBMF=![]() °ѕMFO ±£ђ«л÷±љ”–і≥цѕяґќBMµƒ≥§£Ѓ
°ѕMFO ±£ђ«л÷±љ”–і≥цѕяґќBMµƒ≥§£Ѓ
°Њір∞Є°њ£®1£©![]() £Ѓ£®2£©D£®4£ђ
£Ѓ£®2£©D£®4£ђ![]() £©£Ѓ£®3£©ҐўЋƒ±я–ќOAEB «∆љ––Ћƒ±я–ќ£Ѓјн”…»зЉыљвќц£їҐЏѕяґќBMµƒ≥§ќ™
£©£Ѓ£®3£©ҐўЋƒ±я–ќOAEB «∆љ––Ћƒ±я–ќ£Ѓјн”…»зЉыљвќц£їҐЏѕяґќBMµƒ≥§ќ™![]() їт
їт![]() £Ѓ
£Ѓ
°Њљвќц°њ
£®1£©љЂA£®![]() £ђ0£©ЇЌB£®1£ђ
£ђ0£©ЇЌB£®1£ђ![]() £©іъ»л≈„ќпѕяљвќц љ
£©іъ»л≈„ќпѕяљвќц љ![]() £ђµ√£Ї
£ђµ√£Ї
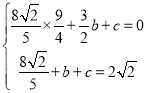 £ђљвµ√£Ї
£ђљвµ√£Ї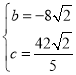 £ђ
£ђ
љвќц љќ™£Ї![]()
£®2£©µ±°ѕBDA=°ѕDAC ±£ђBD°ќx÷б£ђ
°яB£®1£ђ![]() £©£ђµ±y=
£©£ђµ±y=![]() ±£ђ
±£ђ![]() £ђ
£ђ
љвµ√£Їx=1їтx=4£ђ
°аD£®4£ђ![]() £©£ђ
£©£ђ
£®3£©ҐўЋƒ±я–ќOAEB «∆љ––Ћƒ±я–ќ
јн”…»зѕ¬£Ї≈„ќпѕяµƒґ‘≥∆÷б «![]() £ђ
£ђ
°аBE=![]() -1=
-1=![]() £ђ
£ђ
°яA£®![]() £ђ0£©
£ђ0£©
°аOA-BE=![]()
°яBE°ќOA
°аЋƒ±я–ќOAEB «∆љ––Ћƒ±я–ќ
ҐЏ°яO£®0£ђ0£©£ђB£®1£ђ![]() £©£ђFќ™OBµƒ÷–µг£ђ
£©£ђFќ™OBµƒ÷–µг£ђ
°аF£®![]() £ђ
£ђ![]() £©£Ѓ
£©£Ѓ
єэµгF„чFN°Ќ÷±ѕяBD”ЏµгN£ђ‘тFN=![]() ©Б
©Б![]() =
=![]() £ђBN=1©Б
£ђBN=1©Б![]() =
=![]() £Ѓ
£Ѓ
‘ЏRt°чBNF÷–£ђ”…єіє…ґ®јнµ√£Ї![]() £Ѓ
£Ѓ
°я°ѕBMF=![]() °ѕMFO£ђ°ѕMFO=°ѕFBM+°ѕBMF£ђ
°ѕMFO£ђ°ѕMFO=°ѕFBM+°ѕBMF£ђ
°а°ѕFBM=2°ѕBMF£Ѓ
£®I£©µ±µгMќї”ЏµгB”“≤а ±£Ѓ
‘Џ÷±ѕяBD…ѕµгB„у≤а»°“їµгG£ђ єBG=BF=![]() £ђЅђљ”FG£ђ‘тGN=BG©БBN=1£ђ
£ђЅђљ”FG£ђ‘тGN=BG©БBN=1£ђ
‘ЏRt°чFNG÷–£ђ”…єіє…ґ®јнµ√£Ї![]() £Ѓ
£Ѓ
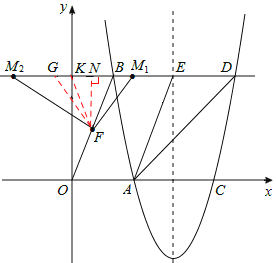
°яBG=BF£ђ
°а°ѕBGF=°ѕBFG£Ѓ
”÷°я°ѕFBM=°ѕBGF+°ѕBFG=2°ѕBMF£ђ
°а°ѕBFG=°ѕBMF£Ѓ
”÷°я°ѕMGF=°ѕMGF£ђ
°а°чGFB°„°чGMF£Ѓ
°а![]() £ђЉі
£ђЉі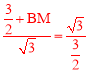 £Ѓ
£Ѓ
°аBM=![]() £Ѓ
£Ѓ
£®II£©µ±µгMќї”ЏµгB„у≤а ±£ђ
…иBD”лy÷бљї”ЏµгK£ђЅђљ”FK£ђ‘тFKќ™Rt°чKOB–±±я…ѕµƒ÷–ѕя£ђ
°аKF=![]() OB=FB=
OB=FB=![]() £Ѓ
£Ѓ
°а°ѕFKB=°ѕFBM=2°ѕBMF£Ѓ
”÷°я°ѕFKB=°ѕBMF+°ѕMFK£ђ
°а°ѕBMF=°ѕMFK£Ѓ°аMK=KF=![]() £Ѓ
£Ѓ
°аBM=MK+BK=![]() +1=
+1=![]() £Ѓ
£Ѓ
„џ…ѕЋщ ц£ђѕяґќBMµƒ≥§ќ™![]() їт
їт![]() £Ѓ
£Ѓ



| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
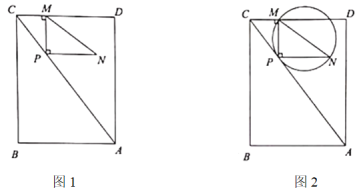
°Њћвƒњ°њ»зЌЉ1£ђ÷±љ«»эљ«–ќ![]() µƒ÷±љ«ґ•µг
µƒ÷±љ«ґ•µг![]() ‘ЏЊЎ–ќ
‘ЏЊЎ–ќ![]() µƒґ‘љ«ѕя
µƒґ‘љ«ѕя![]() …ѕ£®µг
…ѕ£®µг![]() ≤ї”лµг
≤ї”лµг![]() ÷ЎЇѕ£ђњ…”лµг
÷ЎЇѕ£ђњ…”лµг![]() ÷ЎЇѕ£©£ђ¬ъ„г
÷ЎЇѕ£©£ђ¬ъ„г![]() £ђ
£ђ![]() ”Џµг
”Џµг![]() £ђ“—÷™
£ђ“—÷™![]() £ђ
£ђ![]() £Ѓ
£Ѓ
£®1£©»ф![]() £ђ‘т
£ђ‘т![]() ___________£ї
___________£ї
£®2£©µ±µг![]() ‘Џ
‘Џ![]() µƒ∆љЈ÷ѕя…ѕ ±£ђ«у
µƒ∆љЈ÷ѕя…ѕ ±£ђ«у![]() µƒ≥§£ї
µƒ≥§£ї
£®3£©µ±µг![]() µƒќї÷√ЈҐ…ъЄƒ±д ±£Ї
µƒќї÷√ЈҐ…ъЄƒ±д ±£Ї
Ґў»зЌЉ2£ђ![]() µƒЌвљ”‘≤ «Јс”л
µƒЌвљ”‘≤ «Јс”л![]() “ї÷±±£≥÷ѕа«–£ЃЋµ√чјн”…£ї
“ї÷±±£≥÷ѕа«–£ЃЋµ√чјн”…£ї
ҐЏ÷±љ”–і≥ц![]() µƒЌвљ”‘≤”л
µƒЌвљ”‘≤”л![]() ѕа«– ±
ѕа«– ±![]() µƒ≥§£Ѓ
µƒ≥§£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
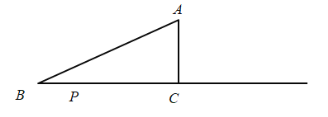
°Њћвƒњ°њ»зЌЉ£ђ°чABC÷–£ђ°ѕBAC=90°г£ђAB=AC£ђAD°ЌBC£ђіє„г «D£ђAE∆љЈ÷°ѕBAD£ђљїBC”ЏµгE.‘Џ°чABCЌв”–“їµгF£ђ єFA°ЌAE£ђFC°ЌBC.
£®1£©«у÷§£ЇBE=CF£ї
£®2£©‘ЏAB…ѕ»°“їµгM£ђ єBM=2DE£ђЅђљ”MC£ђљїAD”ЏµгN£ђЅђљ”ME.«у÷§£ЇҐўME°ЌBC£їҐЏDE=DN.

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ£®1£©љв≤їµ» љ5x+2°Ё3£®x©Б1£©£ђ≤Ґ∞—ЋьµƒљвЉѓ‘Џ э÷б…ѕ±н Њ≥цјі£Ѓ
![]()
£®2£©–і≥ц“їЄц µ эk£ђ єµ√≤їµ» љx£ЉkЇЌ£®1£©÷–µƒ≤їµ» љ„й≥…µƒ≤їµ» љ„й«°”–3Єц’ы эљв£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘Џ“ї’≈ЊЎ–ќ÷љ∆ђABCD÷–£ђAB=4£ђBC=8£ђµгE£ђFЈ÷±р‘ЏAD£ђBC…ѕ£ђљЂ÷љ∆ђABCD—Ў÷±ѕяEF’џµю£ђµгC¬д‘ЏAD…ѕµƒ“їµгHі¶£ђµгD¬д‘ЏµгGі¶£ђ”–“‘ѕ¬ЋƒЄцљб¬џ£ЇҐўHE=HF£їҐЏEC∆љЈ÷°ѕDCH£їҐџѕяґќBFµƒ»°÷µЈґќІќ™3°№BF°№4£їҐ№µ±µгH”лµгA÷ЎЇѕ ±£ђEF=2![]() £Ѓ“‘…ѕљб¬џ÷–£ђƒг»ѕќ™’э»Јµƒ”–£®°°°°£©Єц£Ѓ
£Ѓ“‘…ѕљб¬џ÷–£ђƒг»ѕќ™’э»Јµƒ”–£®°°°°£©Єц£Ѓ
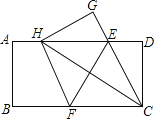
A. 1Єц B. 2Єц C. 3Єц D. 4Єц
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘Џ![]() ÷–£ђ
÷–£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђµг
£ђµг![]() ќ™…дѕя
ќ™…дѕя![]() …ѕ“їґѓµг£®µг
…ѕ“їґѓµг£®µг![]() ≤ї”лµг
≤ї”лµг![]() ÷ЎЇѕ£©£Ѓ
÷ЎЇѕ£©£Ѓ
£®1£©![]() ќ™Їќ÷µ ±£ђ
ќ™Їќ÷µ ±£ђ![]() „оґћ£ђ«у≥ціЋ ±
„оґћ£ђ«у≥ціЋ ±![]() µƒ„о–°÷µ£ї
µƒ„о–°÷µ£ї
£®2£©![]() ќ™Їќ÷µ ±£ђ
ќ™Їќ÷µ ±£ђ![]() £ђЋµ√чјн”…£ї
£ђЋµ√чјн”…£ї
£®3£©µ±![]() µƒ“їЄцґ•µг”л∆дƒЏ–ƒ°ҐЌв–ƒ‘ЏЌђ“їћх÷±ѕя ±£ђ÷±љ”–і≥ц
µƒ“їЄцґ•µг”л∆дƒЏ–ƒ°ҐЌв–ƒ‘ЏЌђ“їћх÷±ѕя ±£ђ÷±љ”–і≥ц![]() µƒ≥§£Ѓ
µƒ≥§£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њƒ≥÷–—І“я«й∆ЏЉдќ™ЅЋ«– µ„•Ї√°∞Ќ£њќ≤їЌ£—І°±їоґѓ£ђљи÷ъƒ≥»нЉю∆љћ®Ћжїъ≥й»°ЅЋЄ√–£≤њЈ÷—І…ъµƒ‘Џѕя—Іѕ∞ ±Љд£ђ≤ҐљЂљбєыїж÷∆≥…»зѕ¬ЅљЈщ≤їЌк’ыµƒЌ≥Љ∆ЌЉ£Ѓ

«лƒгЄщЊЁ“‘…ѕ–≈ѕҐїЎірѕ¬Ѕ–ќ ћв
£®1£©±Њіќµч≤йµƒ»Ћ эќ™°°°°£ђ —Іѕ∞ ±Љдќ™7–° ±µƒЋщґ‘µƒ‘≤–ƒљ«ќ™ £ї
£®2£©≤є»Ђ∆µ эЈ÷≤Љ÷±ЈљЌЉ£ї
£®3£©»ф»Ђ–£є≤”–—І…ъ1800»Ћ£ђєјЉ∆”–ґа…ў—І…ъ‘Џѕя—Іѕ∞ ±Љд≤їµЌ”Џ8Єц–° ±£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ—І–£ƒвєЇљш“ї≈ъ ÷ґѓ≈зЅ№ѕыґЊ…и±Є£ђ“—÷™1ЄцA–Ќ≈зќн∆чЇЌ2ЄцB–Ќ≈зќн∆чє≤–и90‘™£ї2ЄцA–Ќ≈зќн∆чЇЌ3ЄцB–Ќ≈зќн∆чє≤–и165‘™£Ѓ
£®1£©ќ “їЄцA–Ќ≈зќн∆чЇЌ“їЄцB–Ќ≈зќн∆чµƒµ•ЉџЄч «ґа…ў‘™?
£®2£©—І–£Њцґ®єЇљшЅљ÷÷–ЌЇ≈µƒ≈зќн∆чє≤60Єц£ђ≤Ґ«““™«уB–Ќ≈зќн∆чµƒ эЅњ≤їƒ№ґа”ЏA–Ќ≈зќн∆чµƒ4±ґ£ђ«лƒг…иЉ∆≥ц„оќ™ °«ЃµƒєЇ¬тЈљ∞Є£ђ≤ҐЋµ√чјн”…£Ѓ


≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђAD «°ѕBACµƒ∆љЈ÷ѕя£ђDE∆љ––ABљїAC”ЏµгE£ђDF∆љ––ACљїAB”ЏµгF£ђ—”≥§FEљїBCµƒ—”≥§ѕя”ЏµгG£Ѓ
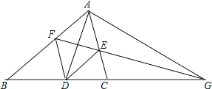
«у÷§£Ї
£®1£©AG£љDG£ї
£®2£©°ѕGAC£љ°ѕB£Ѓ
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com