
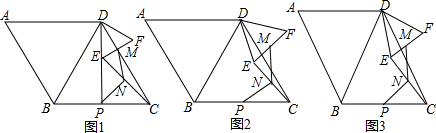
分析 (1)首先根据四边形ABCD是菱形,∠A=60°,判断出△ABD、△BCD是等边三角形;然后判断出∠DME=90°,在Rt△CME中,根据N为EC的中点,求出MN的长是多少即可.
(2)首先连接BE、CF,根据三角形的中位线定理,判断出MN=$\frac{1}{2}CF$,PN=$\frac{1}{2}BE$;然后根据全等三角形判定的方法,判断出△BDE≌△∠CDF,即可判断出CF=BE,所以MN=PN.
(3)∠ABD与∠MNP的和是一个定值,∠ABD+∠MNP=180°.首先连接BE、CF,延长CE交BD于点G,根据三角形的中位线定理,判断出∠MNE=∠FCE=∠FCD+∠DCEM,∠ENP=∠BEG;然后根据全等三角形判定的方法,判断出△BDE≌△∠CDF,即可判断出∠DBE=∠DCF;最后根据三角形的外角的性质,以及三角形的内角和定理,判断出∠ABD+∠MNP=180°即可.
解答 解:(1)如图1,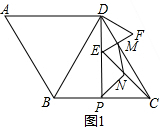 ,
,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
又∵∠A=60°,
∴△ABD是等边三角形,
∴AB=AD=BD,
∴BC=CD=BD,
∴△BCD是等边三角形,
又∵P为BC的中点,
∴DP是∠BDC的平分线,
∴∠CDP=60°÷2=30°,
又∵三角形DEF是等边三角形,
∴∠DEF=60°,
∴∠DME=180°-30°-60°=90°,
在Rt△CME中,
∵N为EC的中点,
∴MN=$\frac{1}{2}CE=\frac{1}{2}×3=\frac{3}{2}$,
即MN的长是$\frac{3}{2}$.
(2)如图2,连接BE、CF,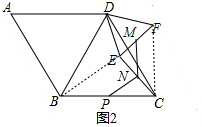 ,
,
∵点N、M分别为EC、EF的中点,
∴MN是△CEF的中位线,
∴MN=$\frac{1}{2}CF$;
∵点N、P分别为EC、BC的中点,
∴PN是△CBE的中位线,
∴PN=$\frac{1}{2}BE$;
∵∠BDC=60°,∠EDF=60°,
∴∠BDC-∠EDC=∠EDF-∠EDC,
即∠BDE=∠CDF,
在△BDE和△∠CDF中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BDE=∠CDF}\\{DE=DF}\end{array}\right.$
∴△BDE≌△∠CDF,
∴CF=BE,
∴MN=PN.
(3)∠ABD与∠MNP的和是一个定值,∠ABD+∠MNP=180°.
证明:如图3,连接BE、CF,延长CE交BD于点G,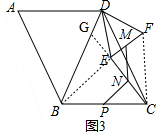 ,
,
∵点N、M分别为EC、EF的中点,
∴MN是△CEF的中位线,
∴MN∥CF,
∴∠MNE=∠FCE=∠FCD+∠DCE,
∵点N、P分别为EC、BC的中点,
∴PN是△CBE的中位线,
∴PN∥BE,
∴∠ENP=∠BEG,
∵AB∥CD,
∴∠BDC=∠ABD,
又∵∠EDF=∠ABD,
∴∠BDC=∠EDF,
∴∠BDC-∠EDC=∠EDF-∠EDC,
即∠BDE=∠CDF,
∵∠A=∠DBC,∠ADB=∠DBC,
∴∠A=∠ADB,
∴AB=BD,
又∵AB=CD,
∴BD=CD,
在△BDE和△∠CDF中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BDE=∠CDF}\\{DE=DF}\end{array}\right.$
∴△BDE≌△∠CDF,
∴∠DBE=∠DCF,
根据三角形的外角的性质,可得
∠BGE=∠BDC+∠DCE,
在△BGE中,
∠BEG+∠BGE+∠GBE=180°,
∴∠ENP+(∠BDC+∠DCE)+∠DCF=180°,
∴(∠ENP+∠DCF+∠DCE)+∠BDC=180°,
又∵∠ENP+∠DCF+∠DCE=∠MNP,∠BDC=∠ABD,
∴∠ABD+∠MNP=180°,
即∠ABD与∠MNP的和是一个定值.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力、空间想象能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS--三条边分别对应相等的两个三角形全等.②判定定理2:SAS--两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA--两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS--两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL--斜边与直角边对应相等的两个直角三角形全等.
(3)此题还考查了三角形中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.
(4)此题还考查了三角形的外角的性质和三角形的内角和定理,要熟练掌握.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
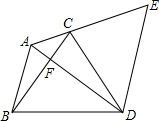 如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.
如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
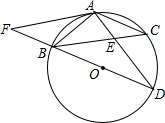 如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.
如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
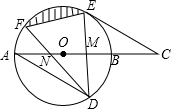 如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C.
如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com