
【题目】如图,在ABCD中,点E,F在对角线AC上,且AE=CF.求证: 
(1)DE=BF;
(2)四边形DEBF是平行四边形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥CB,AD=CB,
∴∠DAE=∠BCF,
在△ADE和△CBF中,
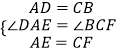
∴△ADE≌△CBF,
∴DE=BF
(2)证明:由(1),可得∴△ADE≌△CBF,
∴∠ADE=∠CBF,
∵∠DEF=∠DAE+∠ADE,∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE,
∴DE∥BF,
又∵DE=BF,
∴四边形DEBF是平行四边形
【解析】(1)根据全等三角形的判定方法,判断出△ADE≌△CBF,即可推得DE=BF.(2)首先判断出DE∥BF;然后根据一组对边平行且相等的四边形是平行四边形,推得四边形DEBF是平行四边形即可.此题主要考查了平行四边形的判定和性质的应用,以及全等三角形的判定和性质的应用,要熟练掌握.


科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,![]() ,设c为最长边.当
,设c为最长边.当![]() 时,△ABC是直角三角形;当
时,△ABC是直角三角形;当![]() 时,利用代数式
时,利用代数式![]() 和
和![]() 的大小关系,可以判断△ABC的形状(按角分类).
的大小关系,可以判断△ABC的形状(按角分类).
(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为____三角形;当△ABC三边长分别为6,8,11时,△ABC为______三角形.
(2)小明同学根据上述探究,有下面的猜想:“当![]() 时,△ABC为锐角三角形;当
时,△ABC为锐角三角形;当![]() 时,△ABC为钝角三角形.” 请你根据小明的猜想完成下面的问题:
时,△ABC为钝角三角形.” 请你根据小明的猜想完成下面的问题:
当![]() ,
,![]() 时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】穿越青海境内的兰新高铁极大地改善了沿线人民的经济文化生活,该铁路沿线甲,乙两城市相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度比普通列车快160km/h,设普通列车的平均行驶速度为xkm/h,依题意,下面所列方程正确的是( )
A.![]() ﹣
﹣ ![]() =4
=4
B.![]() =4
=4
C.![]()
![]() =4
=4
D.![]()
![]() =4
=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC=(填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是
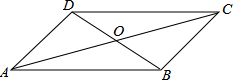
A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A1(2,2)在直线y=x上,过点A1作A1B1∥y轴交直线y= ![]() x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y=
x于点B1 , 以点A1为直角顶点,A1B1为直角边在A1B1的右侧作等腰直角△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线y=x和y= ![]() x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示)
x于A2 , B2两点,以点A2为直角顶点,A2B2为直角边在A2B2的右侧作等腰直角△A2B2C2…,按此规律进行下去,则等腰直角△AnBnCn的面积为(用含正整数n的代数式表示) 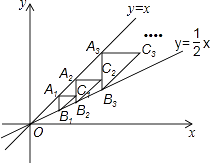
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com