
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,点B坐标为(3,0),对称轴为直线x=1.下列结论正确的是( )
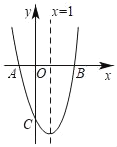
A.abc<0B.b2<4ac
C.a+b+c>0D.当y<0时,﹣1<x<3
【答案】D
【解析】
利用抛物线开口向上得到a>0,由对称轴为直线![]() 得到b=-2a<0,由抛物线与y轴的交点在x轴下方得到c<0,则可对A选项进行判断;利用抛物线与x轴有2个交点,可对B选项进行判断;利用x=1时,y<0可对C选项进行判断;利用抛物线的对称性得A点坐标为(-1,0),通过抛物线在x轴下方对应的自变量的范围可对D选项进行判断.
得到b=-2a<0,由抛物线与y轴的交点在x轴下方得到c<0,则可对A选项进行判断;利用抛物线与x轴有2个交点,可对B选项进行判断;利用x=1时,y<0可对C选项进行判断;利用抛物线的对称性得A点坐标为(-1,0),通过抛物线在x轴下方对应的自变量的范围可对D选项进行判断.
解:∵抛物线开口向上,
∴a>0,
∵对称轴为直线![]() ,
,
∴b=﹣2a<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以A选项错误;
∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,所以B选项错误;
∵x=1时,y<0,
∴a+b+c<0,所以C选项错误;
∵对称轴为直线x=1.
而点B坐标为(3,0),
∴A点坐标为(﹣1,0),
∴当y<0时,﹣1<x<3,所以D选项正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,抛物线 y ax2 bx +3a (a≠0)过点 A(1,0).
(1)求抛物线的对称轴;
(2)直线 y=-x+4 与 y 轴交于点 B,与该抛物线的对称轴交于点 C,现将点 B 向左平移 一个单位到点 D,如果该抛物线与线段 CD有交点,结合函数的图象,求 a 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
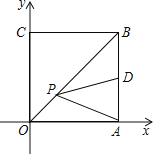
【题目】如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润 = 销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
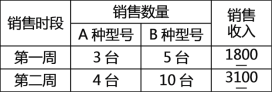
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李叔叔和张阿姨栽树.李叔叔栽6棵树所用的时间与张阿姨栽5棵树所用的时间相同,已知李叔叔比张阿姨平均每天多栽20棵树.
(1)求李叔叔平均每天栽树的棵数;
(2)由李叔叔和张阿姨同时栽树1540棵,要几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《太原市电动自行车管理条例》的规定,2019年5月1日起,未上牌的电动自行车将禁止上路行驶,而电动自行车上牌登记必须满足国家标准.某商店购进了甲.乙两种符合国家标准的新款电动自行车.其中甲种车总进价为22500元,乙种车总进价为45000元,已知乙种车每辆的进价是甲种车进价的1.5倍,且购进的甲种车比乙种车少5辆.
(1)甲种电动自行车每辆的进价是多少元?
(2)这批电动自行车上市后很快销售一空.该商店计划按原进价再次购进这两种电动自行车共50辆,将新购进的电动自行车按照表格中的售价销售.设新购进甲种车m辆(20≤m≤30),两种车全部售出的总利润为y元(不计其他成本).
①求y与m之间的函数关系式;
②商店怎样安排进货方案,才能使销售完这批电动自行车获得的利润最大?最大利润是多少?
型号 | 甲 | 乙 |
售价(元/辆) | 2000 | 2800 |
查看答案和解析>>
科目:初中数学 来源: 题型:
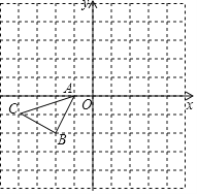
【题目】如图,方格纸中的每个小正方形的边长都为1,在建立平面直角坐标系后,△ABC的顶点均在格点上.
(1)以点A为旋转中心,将△ABC绕点A顺时针旋转90°得到△AB1C1,画出△AB1C1;
(2)画出△ABC关于原点O成中心对称的△A2B2C2,若点B的坐标为(-2,-2),则点B2的坐标为_________.
(3)若△A2B2C2可看作是由△AB1C1绕点P顺时针旋转90°得到的,则点P的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 交于C,D两点,其中点C在y轴上,点D的坐标为
交于C,D两点,其中点C在y轴上,点D的坐标为![]() 。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
。点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
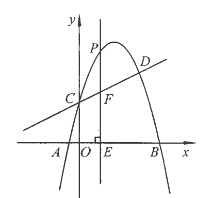
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O,C,P,F为顶点的四边形是平行四边形?请说明理由;
(3)若存在点P,使∠PCF=450,请直接写出相应的点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com