
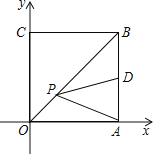
【题目】如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为_____.
【答案】y=﹣2x+8
【解析】
根据正方形的性质得到点A,C关于直线OB对称,连接CD交OB于P,连接PA,PD,则此时,PD+AP的值最小,求得直线CD的解析式为y=﹣![]() x+4,由于直线OB的解析式为y=x,解方程组得到P(
x+4,由于直线OB的解析式为y=x,解方程组得到P(![]() ,
,![]() ),由待定系数法即可得到结论.
),由待定系数法即可得到结论.
解:∵四边形ABCO是正方形,
∴点A,C关于直线OB对称,
连接CD交OB于P,连接PA,PD,
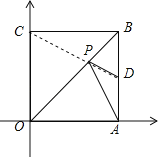
则此时,PD+AP的值最小,
∵OC=OA=AB=4,
∴C(0,4),A(4,0),
∵D为AB的中点,
∴AD=![]() AB=2,
AB=2,
∴D(4,2),
设直线CD的解析式为:y=kx+b,
∴![]() ,
,
∴ ,
,
∴直线CD的解析式为:y=﹣![]() x+4,
x+4,
∵直线OB的解析式为y=x,
∴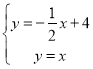 ,
,
解得:x=y=![]() ,
,
∴P(![]() ,
,![]() ),
),
设直线AP的解析式为:y=mx+n,
∴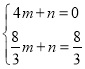 ,
,
解得:![]() ,
,
∴直线AP的解析式为y=﹣2x+8,
故答案为:y=﹣2x+8.


科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 为检测我市正在销售的酸奶质量,应该采用普查的方式
B. 若两名同学连续五次数学测试的平均分相同,则方差较大的同学数学成绩更稳定
C. 抛掷一个正方体骰子,朝上的面的点数为奇数的概率是![]()
D. “打开电视,正在播放广告”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲乙两个玩具小汽车在笔直的240米跑道![]() 上进行折返跑游戏,甲从点
上进行折返跑游戏,甲从点![]() 出发,匀速在
出发,匀速在![]() 、
、![]() 之间折返跑,同时乙从点
之间折返跑,同时乙从点![]() 出发,以大于甲的速度匀速在
出发,以大于甲的速度匀速在![]() 、
、![]() 之间折返跑.在折返点的时间忽略不计.
之间折返跑.在折返点的时间忽略不计.

(1)若甲的速度为![]() ,乙的速度为
,乙的速度为![]() ,第一次迎面相遇的时间为
,第一次迎面相遇的时间为![]() ,则
,则![]() 与
与![]() 的关系式___________;
的关系式___________;
(注释:当两车相向而行时相遇是迎面相遇,当两车在![]() 点相遇时也视为迎面相遇)
点相遇时也视为迎面相遇)
(2)如图1,
①若甲乙两车在距![]() 点20米处第一次迎面相遇,则他们在距
点20米处第一次迎面相遇,则他们在距![]() 点_______米第二次迎面相遇:
点_______米第二次迎面相遇:
②若甲乙两车在距![]() 点50米处第一次迎面相遇,则他们在距
点50米处第一次迎面相遇,则他们在距![]() 点__________米第二次迎面相遇;
点__________米第二次迎面相遇;
(3)设甲乙两车在距![]() 点
点![]() 米处第一次迎面相遇,在距
米处第一次迎面相遇,在距![]() 点
点![]() 米处第二次迎面相遇.某同学发现了
米处第二次迎面相遇.某同学发现了![]() 与
与![]() 的函数关系,并画出了部分函数图象(线段
的函数关系,并画出了部分函数图象(线段![]() ,不包括点
,不包括点![]() ,如图2所示).
,如图2所示).
①则![]() _______,并在图2中补全
_______,并在图2中补全![]() 与
与![]() 的函数图象(在图中注明关键点的数据);
的函数图象(在图中注明关键点的数据);
②分别求出各部分图象对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
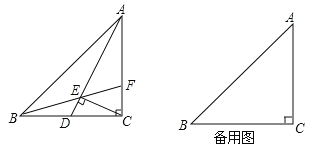
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,D为CB边上一动点,
,D为CB边上一动点,![]() ,连接AD,
,连接AD,![]() 于点E,延长线BE交AC于点F.
于点E,延长线BE交AC于点F.
(1)若![]() ,则
,则![]() ______,
______,![]() ______;
______;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)若F为AC的中点,请直接写出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
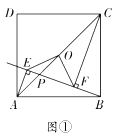
【题目】如图①,已知点![]() 为正方形
为正方形![]() 的对角线的交点,点
的对角线的交点,点![]() 是对角线
是对角线![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() 重合),分别过点
重合),分别过点![]() 向直线
向直线![]() 作垂线,垂足分别为点
作垂线,垂足分别为点![]() ,连接
,连接![]() 和
和![]() .
.

(1)求证:![]() ;
;
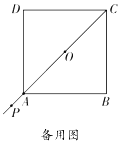
(2)如图②,延长正方形对角线![]() ,当点
,当点![]() 运动到
运动到![]() 的延长线上时,通过证明判断(1)中的结论是否仍然成立;
的延长线上时,通过证明判断(1)中的结论是否仍然成立;
(3)若点![]() 在射线
在射线![]() 上运动,
上运动,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
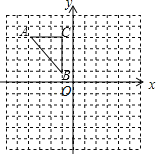
【题目】如图,△ABC在平面直角坐标系中,顶点的坐标分别为A(-4,4),B(-1,1),C(-1,4).
(1)画出与△ABC关于y轴对称的△A1B1C1.
(2)将△ABC绕点B逆时针旋转90°,得到△A2BC2,画两出△A2BC2.
(3)求线段AB在旋转过程中扫过的图形面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
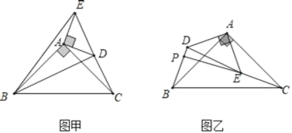
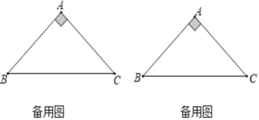
(1)如图甲,将△ADE绕点A旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是哪几个 .(回答直接写序号)
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)
(2)若AB=6,AD=3,把△ADE绕点A旋转:
①当∠CAE=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,点B坐标为(3,0),对称轴为直线x=1.下列结论正确的是( )
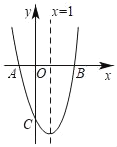
A.abc<0B.b2<4ac
C.a+b+c>0D.当y<0时,﹣1<x<3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,国庆期间,北京举办“普天同庆共筑中国梦”的游园活动,为此,某公园在中央广场处建了一个人工喷泉,如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2m,喷出水流的运动路线是抛物线.如果水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3.6m,求水流的落地点C到水枪底部B的距离.
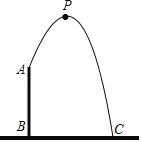
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com