
【题目】下列说法中,正确的是( )
A. 为检测我市正在销售的酸奶质量,应该采用普查的方式
B. 若两名同学连续五次数学测试的平均分相同,则方差较大的同学数学成绩更稳定
C. 抛掷一个正方体骰子,朝上的面的点数为奇数的概率是![]()
D. “打开电视,正在播放广告”是必然事件
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据![]() 参与问卷调查的每名学生只能选择其中一项
参与问卷调查的每名学生只能选择其中一项![]() ,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:

![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
![]() 若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() (x+m)(x﹣4)(m>0)交x轴于点A、B(A左B右),交y轴于点C,过点B的直线y=
(x+m)(x﹣4)(m>0)交x轴于点A、B(A左B右),交y轴于点C,过点B的直线y=![]() x+b交y轴于点D.
x+b交y轴于点D.

(1)求点D的坐标;
(2)把直线BD沿x轴翻折,交抛物线第二象限图象上一点E,过点E作x轴垂线,垂足为点F,求AF的长;
(3)在(2)的条件下,点P为抛物线上一点,若四边形BDEP为平行四边形,求m的值及点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖的奶奶想用铁丝网在自家门前围一块面积为4平方米的矩形菜园,并且用最少的铁丝网,因此小颖进行了如下探究活动.
活动一:(1)设矩形菜园的一边长为x米,铁丝网长为y米.
①用含x的代数式表示矩形菜园另一边长为_____________米;
②y关于x的函数解析式是______________
活动二:(2)①列表:根据(1)中所求的函数关系式计算并补全下图.(y精确到0.1)

②描点:根据表中数值,在平面直角坐标系中描出①中剩下的两个点(x,y).
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考:(3)①请你根据函数图象,写出该函数的两条性质或结论.
②根据以上信息可得,当x=_____________时,y有最小值.由此可知,小颖的奶奶至少需要买_____________米的铁丝网.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡水蜜桃享誉海内外,老王用3000元购进了一批水蜜桃.第一天,很快以比进价高40% 的价格卖出150千克.第二天,他发现剩余的水蜜桃卖相已不太好,于是果断地以比进价低20%的价格将剩余的水蜜桃全部售出,本次生意老王一共获利750元.
(1)根据以上信息,请你编制一个问题,并给予解答;
(2)老王用3000元按第一次的价格又购进了一批水蜜桃.第一天同样以比进价高40% 的价格卖出150千克,第二天,老王把卖相不好的水蜜桃挑出,单独打折销售,售价为10元/千克,结果很快被一抢而空,其余的仍按第一天的价格销售,且当天全部售完.若老王这次至少获利1100元,请问打折销售的水蜜桃最多多少千克?(精确到1千克.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,抛物线 y ax2 bx +3a (a≠0)过点 A(1,0).
(1)求抛物线的对称轴;
(2)直线 y=-x+4 与 y 轴交于点 B,与该抛物线的对称轴交于点 C,现将点 B 向左平移 一个单位到点 D,如果该抛物线与线段 CD有交点,结合函数的图象,求 a 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
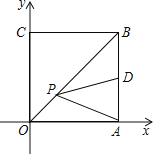
【题目】如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com