练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，已知△ABC中，D、E、F分别是各边的中点，AF平分∠BAC．
    （1）试证明四边形ADFE是菱形．
    （2）△ABC满足什么条件时，四边形ADFE是正方形．
    考点：正方形的判定,三角形中位线定理,菱形的判定
    专题：
    分析：（1）根据题意可得四边形ADFE是平行四边形，由AF平分∠BAC，得四边形ADFE是菱形；
    （2）由（1）已经证明四边形ADFE是菱形，又有一角为直角的菱形是正方形，所以当△ABC是直角三角形时，四边形ADFE是正方形．
    解答：解：∵DF∥CA，EF∥BA，
    ∴四边形ADFE是平行四边形；
    ∵AF平分∠BAC，
    ∴∠EAF=∠FAD，
    ∴∠FAD=∠AFD，
    ∴AD=DF，
    ∴四边形ADFE是菱形；

    （2）当∠BAC=90°时，四边形ADFE是正方形．
    点评：考查了菱形及正方形的判定，牢记菱形的三个判定定理及定义是解答本题的关键，难度一般．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，摆放有五杂梅花，下列说法错误的是（以中心梅花为初始位置）（　　）
    A、左上角的梅花只需沿对角线平移即可
    B、右上角的梅花需先沿对角线平移后，再顺时针旋转45°
    C、右下角的梅花需先沿对角线平移后，再顺时针旋转180
    D、左下角的梅花需先沿对角线平移后，再顺时针旋转90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，BC边上的垂直平分线DE交BC于点D，交AC于点E，AB=4cm，AC=8cm，求△ABE的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为88°、30°，则∠ACB的大小为（　　）
    A、15°B、28°
    C、29°D、34°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    甲、乙、丙三位同学在九年级上学期的五次数学测验中，他们的成绩的平均分都是90分（总分120分），方差分别是S甲2=15.7，S乙2=10.6，S丙2=13.2，则三人中成绩最稳定的是（　　）
    A、甲B、乙C、丙D、不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC中，∠C=90°，BC=2，AB=3，则sinA的值是（　　）
    A、
    3
    2
    B、
    2
    3
    C、
    		5
    3
    D、
    2
    		5
    5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某校研究性学习小组测量学校旗杆AB的高度，如图在教学楼一楼C处测得旗杆顶部的仰角为60°，在教学楼三楼D处测得旗杆顶部的仰角为30°，旗杆底部与教学楼一楼在同一水平线上，已知CD=6米，则旗杆AB的高度为（　　）
    A、9米
    B、9（1+
    		3
    ）米
    C、12米
    D、18米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

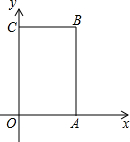    如图，矩形OABC中，O为直角坐标系的原点，A、C两点的坐标分别为（3，0）、（0，5）．
    （1）直接写出B点坐标；
    （2）若过点C的一条直线把矩形OABC的周长分为3：5两部分，求这条直线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程组：
    （1）
     x+2y=5
     3x-2y=3

    （2）
    4y-(4x+10)=30
    3x+6(y+2)=36
    ．

    查看答案和解析>>

    同步练习册答案