
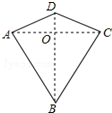
 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 先证明△ABD与△CBD全等,再证明△AOD与△COD全等即可判断.
解答 解:在△ABD与△CBD中,
$\left\{\begin{array}{l}{AD=CD}\\{AB=BC}\\{DB=DB}\end{array}\right.$,
∴△ABD≌△CBD(SSS),
故③正确;
∴∠ADB=∠CDB,
在△AOD与△COD中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADB=∠CDB}\\{OD=OD}\end{array}\right.$,
∴△AOD≌△COD(SAS),
∴∠AOD=∠COD=90°,AO=OC,
∴AC⊥DB,
故①②正确.
故选:D.
点评 此题考查了全等三角形的判定和性质,关键是根据SSS证明△ABD与△CBD全等和利用SAS证明△AOD与△COD全等.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
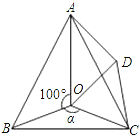 如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△BOC≌△ADC,连接OD.
如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△BOC≌△ADC,连接OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆货车从甲地开往乙地,一辆客车从乙地开往甲地,客车先出发45分钟后,货车出发.如图是货车和客车离甲地的距离y货、y客(km)与货车行驶的时间x(h)之间的函数关系图象,根据图象回答下列问题:
一辆货车从甲地开往乙地,一辆客车从乙地开往甲地,客车先出发45分钟后,货车出发.如图是货车和客车离甲地的距离y货、y客(km)与货车行驶的时间x(h)之间的函数关系图象,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米,
如图,某市对位于笔直公路上的两个小区A、B的供水路线进行优化改造,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区B到供水站M的距离为300米,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图在△ABC中,点D、E分别是AB、AC边上的定点,请你在BC边上确定一点P,使△PDE的周长最小(在图中作出点P,保留作图痕迹,不写作法)
如图在△ABC中,点D、E分别是AB、AC边上的定点,请你在BC边上确定一点P,使△PDE的周长最小(在图中作出点P,保留作图痕迹,不写作法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com