
分析 先将$\sqrt{12}$化简为2$\sqrt{3}$,从而得到a2-1=3,从而可求得a2=4,故此可求得a2+5=9,从而可知$\sqrt{{a}^{2}+5}$=3,最后根据算术平方根的定义求解即可.
解答 解:$\sqrt{12}$=$\sqrt{4×3}$=2$\sqrt{3}$.
∴a2-1=3.
∴a2=4.
∴a2+5=9.
∴$\sqrt{{a}^{2}+5}$=$\sqrt{9}$=3.
∵3的算术平方根是$\sqrt{3}$,
∴$\sqrt{{a}^{2}+5}$的算术平方根是$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题主要考查的是同类二次根式的定义,依据二次根式$\sqrt{12}$化简后的被开方数与$\sqrt{{a}^{2}-1}$的被开方数相同求得a2=4是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
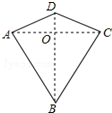 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=$\frac{1}{2}$AC;③△ABD≌△CBD,其中正确的结论有( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.
如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8$\sqrt{3}$m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,则旗杆AB的髙度是( )m.| A. | 8$\sqrt{6}$+24 | B. | 8$\sqrt{6}$+8 | C. | 24+8$\sqrt{3}$ | D. | 8+8$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com