练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．设不等式（m+n）x+（2m-3n）＞0的解集是x＜-$\frac{1}{3}$，求关于x的不等式（m-3n）x＜2m-n的解集．

    分析 根据不等式的解集，可得m、n的值，根据解不等式组的步骤，可得答案．

    解答 解：∵不等式（m+n）x+（2m-3n）＞0的解集是x＜-$\frac{1}{3}$，
    ∴-$\frac{2m-3n}{m+n}$=-$\frac{1}{3}$，
    ∴m+n=-3a，2m-3n=-a，（a＞0），
    解$\left\{\begin{array}{l}{m+n=-3a}\\{2m-3n=-a}\end{array}\right.$，得$\left\{\begin{array}{l}{m=-2a}\\{n=-a}\end{array}\right.$，
    把m=-2a，n=-a代入（m-3n）x＜2m-n得
    ax＜-3a，
    x＜-3，
    ∴关于x的不等式（m-3n）x＜2m-n的解集是x＜-3．

    点评 本题考查了不等式的解集，先求出m、n的值，再求出不等式的解集．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．计算：${（{\sqrt{3}-\sqrt{2}}）^2}-\sqrt{3}（{\sqrt{2}-\sqrt{3}}）$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：
    （1）$\sqrt{24}$$+\sqrt{0.5}$$-（\sqrt{\frac{1}{8}}+\sqrt{6}）$
    （2）3$\sqrt{2}$$-2\sqrt{12}-4\sqrt{\frac{1}{8}}$$+3\sqrt{48}$
    （3）$\frac{2}{3}\sqrt{9x}$+6$\sqrt{\frac{x}{4}}$-2x$\sqrt{\frac{1}{x}}$
    （4）$\sqrt{{a}^{2}b}$$+a\sqrt{\frac{b}{a}}$$-b\sqrt{\frac{a}{b}}$$-\sqrt{a{b}^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．化简．
    （1）$\sqrt{1\frac{15}{49}}$
    （2）$\sqrt{\frac{7}{100}}$
    （3）$\sqrt{\frac{25{a}^{4}}{9{b}^{2}}}$（a＞0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．若点P（2，7）在函数y=ax2+b的图象上，且当x=$\sqrt{3}$时y=5．
    （1）求a，b的值；
    （2）如果点（$\frac{1}{2}$，m）和点（n，1）也在此函数图象上，求m，n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．若二次根式$\sqrt{12}$化简后的被开方数与$\sqrt{{a}^{2}-1}$的被开方数相同，则$\sqrt{{a}^{2}+5}$的算术平方根是$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．若2x=3，2y=6，2z=12，求证：x+z=2y．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

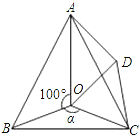    4．如图，点O是等边△ABC内一点，∠AOB=100°，∠BOC=α，D是△ABC外一点，且△BOC≌△ADC，连接OD．
    （1）△COD是什么三角形？说明理由；
    （2）若AO=n2+1，AD=n2-1，OD=2n（n为大于1的整数），求α的度数．
    （3）当α为多少度时，△AOD是等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知∠ABC=90°，D是直线AB上的点，AD=BC，如图，过点A作AF⊥AB，并截取AF=BD，连接DC、DF、CF．
    （1）求证：△FAD≌△DBC；
    （2）判断△CDF的形状并证明．

    查看答案和解析>>

    同步练习册答案