
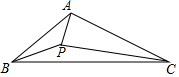
 在△ABC中,∠ABC=40°,∠ACB=30°,P是∠ABC的平分线上一点,∠PCB=10°,求∠PAB.
在△ABC中,∠ABC=40°,∠ACB=30°,P是∠ABC的平分线上一点,∠PCB=10°,求∠PAB. 分析 在BA延长线上取一点D,使BD=BC,连DP,DC.根据BP平分∠ABC,可知C点与点D关于BP对称,得到PD=PC,根据等腰三角形的性质得到∠PDC=∠PCD,∠BDC=∠BCD,等量代换得到∠ADP=∠BCP,根据外角的性质得到∠DPC=2(∠PBC+∠PCB)=60°,推出△PDC是正三角形,得到PC=DC,根据等腰三角形的判定得到AC=PC,根据三角形的内角和即可得到结论.
解答  解:在BA延长线上取一点D,使BD=BC,连DP,DC.
解:在BA延长线上取一点D,使BD=BC,连DP,DC.
∵BP平分∠ABC,可知C点与点D关于BP对称,
∴PD=PC,
∴∠PDC=∠PCD,
∵BD=BC,
∴∠BDC=∠BCD,
∴∠ADP=∠BCP,
∵∠DPC=2(∠PBC+∠PCB)=60°,
∴△PDC是正三角形,
∴PC=DC,
在△ACD中,
∵∠ADC=70°=∠BAC,∴AC=DC,∴AC=PC,
在△PCA中,
∵∠PCA=20°,
∴∠PAC=80°.
∴∠PAB=∠BAC-∠PCA=110°-80°=30°.
点评 本题考查了三角形的内角和,等腰三角形的判定和性质,轴对称的性质,正确的作出辅助线是解题的关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:选择题
 如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )
如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )| A. | 50 | B. | 58 | C. | 68 | D. | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=-2,b=-3 | B. | a=2,b=3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-1 | B. | k≥-1 | C. | k≠0 | D. | k>-1且k≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com