
【题目】为了解某校九年级男生在体能测试的引体向上项目的情况,随机抽取了部分男生引体向上项目的测试成绩,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
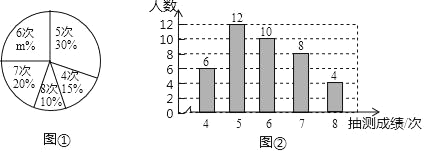
(Ⅰ)本次接受随机抽样调查的男生人数为 ,图①中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)若规定引体向上6次及以上(含6次)为该项目良好,根据样本数据,估计该校320名九年级男生中该项目良好的人数.
【答案】(Ⅰ) 40;25;(Ⅱ)平均数为5.8次;众数为5;中位数为6;(Ⅲ)176名.
【解析】
(Ⅰ)用5次的人数除以5次的人数所占百分比即可得抽查的总人数;求出6次的人数与总人数的比即可得m的值;(Ⅱ)根据平均数、众数和中位数的定义求解即可;(Ⅲ)先求出6次及以上的学生所占的百分比,用320乘以这个百分比即可得答案.
(Ⅰ)12÷30%=40(名);
![]() ×100%=25%,
×100%=25%,
∴m=25,
故答案为:40;25
(Ⅱ)平均数为:(6×4+12×5+10×6+8×7+4×8)÷40=5.8(次)
∵这组数据中,5出现了12次,出现次数最多,
∴这组数据的众数为5,
∵将这组数据从小到大排列,其中处于中间的两个数都是6,
∴![]() =6,即中位数为6,
=6,即中位数为6,
(Ⅲ)6次及以上的学生人数为10+8+4=22(名)
∴![]() ×320=176(名)
×320=176(名)
答:估计该校![]() 名九年级男生中该项目良好的人数为176名.
名九年级男生中该项目良好的人数为176名.


科目:初中数学 来源: 题型:
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.

查看答案和解析>>
科目:初中数学 来源: 题型:
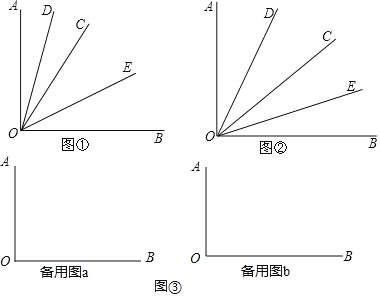
【题目】已知:∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,求∠DOE的度数.
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
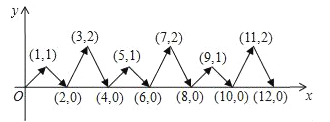
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从顶点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…按这样的运动规律,经过第2010次运动后,动点P的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形桌子可坐6人,按下图方式讲桌子拼在一起.
 ………
………
① ② ③
(1)观察图形,填写下表:
图形(n) | ② | ③ | …… | n |
坐的人数(人) | …… |
(2)一家餐厅有40张这样的长方形桌子,按照上图的方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改为每8张桌子拼成1张大桌子,则共可坐多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量![]() (个)与加工时间
(个)与加工时间![]() (分)之间的函数关系,观察图象解决下列问题:
(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是________,B点表示的实际意义是___________ _____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
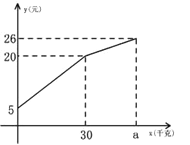
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
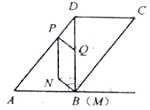
【题目】如图,BD是□ABCD的对角线,AB⊥BD,BD=8cm,AD=10cm,动点P从点D出发,以5cm/s的速度沿DA运动到终点A,同时动点Q从点B出发,沿折线BD—DC运动到终点C,在BD、DC上分别以8cm/s、6cm/s的速度运动.过点Q作QM⊥AB,交射线AB于点M,连接PQ,以PQ与QM为边作□PQMN.设点P的运动时间为t(s)(t>0),□PQMN与□ABCD重叠部分图形的面积为S(cm2).
(1)AP=_______cm(同含t的代数式表示).
(2)当点N落在边AB上时,求t的值.
(3)求S与t之间的函数关系式.
(4)连结NQ,当NQ与△ABD的一边平行时,直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com