
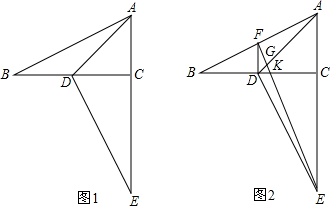
分析 (1)由旋转的性质得出CD=AC,CE=BC,∠DCE=∠ACB=90°,由已知条件得出CE=BC=2AC=2CD,BD=CD,设CD=AC=x,则CE=BC=2x,AE=AC+CE=3x,由勾股定理得出AD=$\sqrt{2}$x,即可得出结果;
(2)证出DF∥AC,得出BF=AF,证出DF是△ABC的中位线,由三角形中位线定理得出DF∥AC,DF=$\frac{1}{2}$AC,得出AE=6DF,CE=4DF,由平行线分线段成比例定理得出$\frac{FG}{GE}=\frac{DF}{AE}=\frac{1}{6}$,$\frac{DK}{CK}$=$\frac{FK}{KE}=\frac{DF}{CE}=\frac{1}{4}$,得出$\frac{KG}{EF}=\frac{2}{35}$;
(3)作KM⊥DE于M,设DK=a,则CK=4a,CD=5a,CE=10a,由勾股定理得出DE=5$\sqrt{5}$a,KE2=CK2+CE2=116a2,由△DEK的面积=$\frac{1}{2}$DE•KM=$\frac{1}{2}$DK•CE,求出KM=$\frac{2\sqrt{5}}{5}$a,由勾股定理求出ME,再由三角函数即可得出结果.
解答 解:(1)由旋转的性质得:CD=AC,CE=BC,∠DCE=∠ACB=90°,
∵2AC=BC,
∴CE=BC=2AC=2CD,BD=CD,
设CD=AC=x,则CE=BC=2x,
∴AE=AC+CE=3x,
由勾股定理得:AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{2}$x,
∴$\frac{AE}{AD}$=$\frac{3x}{\sqrt{2}x}$=$\frac{3\sqrt{2}}{2}$;
(2)∵DF⊥BC,∠ACB=90°,
∴DF∥AC,
∵BD=CD,
∴BF=AF,
∴DF是△ABC的中位线,
∴DF∥AC,DF=$\frac{1}{2}$AC,
∴AE=6DF,CE=4DF,$\frac{FG}{GE}=\frac{DF}{AE}=\frac{1}{6}$,$\frac{DK}{CK}$=$\frac{FK}{KE}=\frac{DF}{CE}=\frac{1}{4}$,
∴$\frac{FG}{EF}=\frac{1}{7}$=$\frac{5}{35}$,$\frac{FK}{EF}=\frac{1}{5}$=$\frac{7}{35}$,
∴$\frac{KG}{EF}=\frac{2}{35}$;
(3)作KM⊥DE于M,如图所示;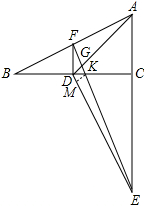
则∠KME=90°,
设DK=a,则CK=4a,
∴CD=5a,CE=10a,
由勾股定理得:DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=5$\sqrt{5}$a,KE2=CK2+CE2=116a2,
∵△DEK的面积=$\frac{1}{2}$DE•KM=$\frac{1}{2}$DK•CE,
∴5$\sqrt{5}$a•KM=a×10a,
解得:KM=$\frac{2\sqrt{5}}{5}$a,
∴ME=$\sqrt{K{E}^{2}-K{M}^{2}}$=$\sqrt{116{a}^{2}-(\frac{2\sqrt{5}}{5})^{2}}$=$\frac{24\sqrt{5}}{5}$,
∴tan∠DEF=$\frac{KM}{ME}$=$\frac{\frac{2\sqrt{5}}{5}}{\frac{24\sqrt{5}}{5}}$=$\frac{1}{12}$;
故答案为:$\frac{1}{12}$.
点评 本题考查了旋转的性质、勾股定理、三角形中位线定理、平行线分线段成比例定理、比例的性质、三角形面积的计算方法、三角函数等知识;本题综合性强,难度较大,特别是(3)中,需要通过作辅助线运用勾股定理和三角函数才能得出结果.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
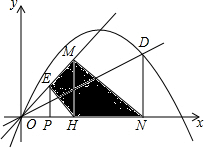 如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线y=-$\frac{1}{4}{x}^{2}+nx$交于点D,直线OD的解析式为y=$\frac{1}{2}x$.点P(x,0)是x轴上一动点,过点P作y轴的平行线,交射线OM于点E.
如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线y=-$\frac{1}{4}{x}^{2}+nx$交于点D,直线OD的解析式为y=$\frac{1}{2}x$.点P(x,0)是x轴上一动点,过点P作y轴的平行线,交射线OM于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
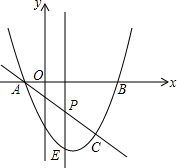 如图,抛物线y=x2-2x-3与x轴交A,B两点(A点在B点左侧),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A,B两点(A点在B点左侧),直线l与抛物线交于A,C两点,其中C点的横坐标为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
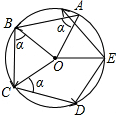 如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?
如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com