
【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.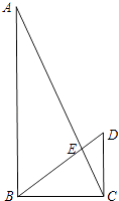
(1)求BE的长度;
(2)求△ABE的面积.
【答案】
(1)解:∵CD⊥BC,
∴∠DCB=90°,
在Rt△BCD中,BC=4,DC=3,
根据勾股定理得:BD= ![]() =5,
=5,
∵AB∥CD,
∴△ABE∽△CDE,
∴DC:AB=DE:BE=3:9=1:3,
又∵BD=5,
∴BE= ![]() BD=
BD= ![]()
(2)解:作EF⊥AB,EH⊥CD,
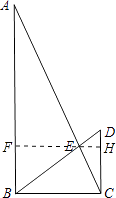
∵△ABE∽△CDE,
∴EF:EH=DC:AB=1:3,
又∵BC=4,
∴FE= ![]() BC=3,EF的长,
BC=3,EF的长,
则S△ABE=AB×EF× ![]() =
= ![]() .
.
【解析】(1)在Rt△BCD中根据勾股定理得出BD的长,根据平行于三角形一边的直线截其它两边的延长线,所截得的三角形与原三角形相似得出△ABE∽△CDE,根据相似三角形对应边成比例得出DC:AB=DE:BE=3:9=1:3,从而得出答案;
(2)作EF⊥AB,EH⊥CD,根据相似三角形对应高的比等于相似比得出EF的长,从而根据三角形的面积公式计算即可。
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


科目:初中数学 来源: 题型:
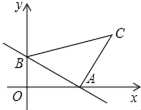
【题目】一次函数y=﹣![]() x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )
x+2的图象与x轴,y轴分别交于A、B两点,以AB为腰,作等腰Rt△ABC,则直线BC的解析式为( )
A. y=![]() x+2 B. y=﹣
x+2 B. y=﹣![]() x+2 C. y=﹣
x+2 C. y=﹣![]() x+2 D. y=
x+2 D. y=![]() x+2
x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数0,B点表示的数是最小的正整数,C点表示数5,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.

(1) BC= .
(2) A,B,C在数轴上同时运动,点B和点C分别以每秒3个单位长度和6个单位长度的速度向右运动,点A以每秒a个单位长度的速度向左运动。在运动过程中,3BC-2AB的值始终保持不变,请求出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国足球改革总体方案》提出足球要进校园,为了解某校学生对校园足球喜爱的情况,随机对该校部分学生进行了调查,将调查结果分为“很喜欢”、“较喜欢”、“一般”、“不喜欢”四个等级,并根据调查结果绘制成了如下两幅不完整的统计图;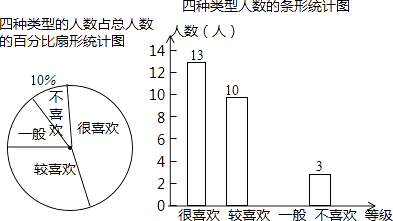
(1)一共调查了名学生,请补全条形统计图;
(2)在此次调查活动中,选择“一般”的学生中只有两人来自初三年级,现在要从选择“一般”的同学中随机抽取两人来谈谈各自对校园足球的感想,请用画树状图或列表法求选中的两人刚好都来自初三年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
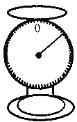
【题目】某市场的公平秤如图,把10千克的菜放到秤上,指示盘上的指针转了180°.
(1)如果把2.75千克的菜放在秤上,指针转过多少度?
(2)如果称好0.5千克的菜没有拿走,再把一捆菜放在秤上,指针共转了![]() 那么,后放上的这捆菜有多少千克?
那么,后放上的这捆菜有多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一位旅行者在早晨8时从城市出发到郊外所走路程与时间的变化图.根据图回答问题:
(1)9时,10时30分,12时所走的路程分别是多少千米?
(2)他中途休息了多长时间?
(3)他从休息后直达目的地这段时间的速度是多少?(列式计算)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com