
【题目】如图为一位旅行者在早晨8时从城市出发到郊外所走路程与时间的变化图.根据图回答问题:
(1)9时,10时30分,12时所走的路程分别是多少千米?
(2)他中途休息了多长时间?
(3)他从休息后直达目的地这段时间的速度是多少?(列式计算)

 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程s(km) | 0 | 100 | 200 | 300 | 400 | … |
油箱剩余油量Q(L) | 50 | 42 | 34 | 26 | 18 | … |
(1)该轿车油箱的容量为______L,行驶150km时,油箱剩余油量为______L;
(2)根据上表的数据,写出油箱剩余油量Q(L)与轿车行驶的路程s(km)之间的表达式;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.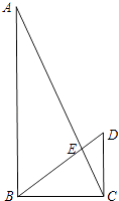
(1)求BE的长度;
(2)求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,EF与BD交于G,且∠DEF=60°,若AD=3,AE=2,则sin∠BEF= . 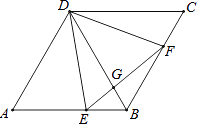
查看答案和解析>>
科目:初中数学 来源: 题型:
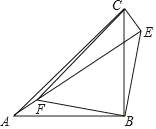
【题目】如图,点E是等腰三角形纸片ABC外一点,∠ABC=90°,连接AE,点F是线段AE(不与点A,E重合)上一点,在△EBF中,EB=FB,∠EBF=90°,连接CE,CF
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,D在BC的延长线上,∠ABC与∠ACD的平分线相交于点P,则下列结论中不一定正确的是( )
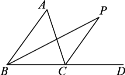
A. ∠ACD=2∠A B. ∠A=2∠P C. BP⊥AC D. BC=CP
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,点C将线段AB分成两部分(AC>BC),如果 ![]() =
= ![]() ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果
,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果 ![]() =
= ![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.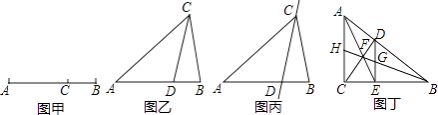
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有2个完全相同的小球,分别标有数字﹣1,﹣2.现从甲袋中随机抽取一个小球,将标有的数字记录为x,再从乙袋中随机抽取一个小球,将标有的数字记录为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在二次函数y=x2﹣2x﹣2的图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com