
【题目】如图甲,点C将线段AB分成两部分(AC>BC),如果 ![]() =
= ![]() ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果
,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果 ![]() =
= ![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.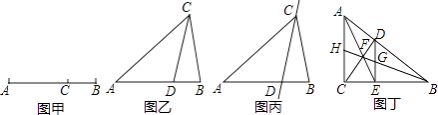
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由.
【答案】
(1)解:点D是AB边上的黄金分割点.理由如下:
∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵CD是角平分线,
∴∠ACD=∠BCD=36°,
∴∠A=∠ACD,
∴AD=CD,
∵∠CDB=180°﹣∠B﹣∠BCD=72°,
∴∠CDB=∠B,
∴BC=CD,
∴BC=AD.
在△BCD与△BCA中,∠B=∠B,∠BCD=∠A=36°,
∴△BCD∽△BAC,
∴ ![]() ,
,
∴ ![]() ,
,
∴点D是AB边上的黄金分割点.
(2)直线CD是△ABC的黄金分割线.理由如下:
证明:设△ABC中,AB边上的高为h,则S△ABC= ![]() ABh,S△ACD=
ABh,S△ACD= ![]() ADh,S△BCD=
ADh,S△BCD= ![]() BDh,
BDh,
∴S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,
由(1)知,点D是AB边上的黄金分割点,
∴ ![]() ,
,
∴S△ACD:S△ABC=S△BCD:S△ACD,
∴CD是△ABC的黄金分割线.
(3)解:直线BH不是△ABC的黄金分割线.理由如下:
∵DE∥AC,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴AH2=HC2,
∴AH=HC,
∴S△BHA=S△BHC= ![]() S△ABC,
S△ABC,
∴BH不是△ABC的黄金分割线.
【解析】(1)根据等边对等角得出∠B=∠ACB=72°,根据角平分线的定义及等量代换得出∠A=∠ACD,进而根据等角对等边得出AD=CD,BC=CD,从而得出BC=AD.然后判断出△BCD∽△BAC,根据相似三角形对应边成比例得出![]() =
=![]() ,从而得出
,从而得出![]() =
=![]() ,从而得出结论点D是AB边上的黄金分割点;
,从而得出结论点D是AB边上的黄金分割点;
(2)设△ABC中,AB边上的高为h,根据三角形的面积公式,则S△ABC= ![]() ABh,S△ACD=
ABh,S△ACD= ![]() ADh,S△BCD=
ADh,S△BCD= ![]() BDh,故S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,由(1)知,点D是AB边上的黄金分割点,故
BDh,故S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,由(1)知,点D是AB边上的黄金分割点,故![]() =
=![]() ,根据等量代换得S△ACD:S△ABC=S△BCD:S△ACD,从而得出结论;
,根据等量代换得S△ACD:S△ABC=S△BCD:S△ACD,从而得出结论;
(3)直线BH不是△ABC的黄金分割线.理由如下:根据平行线分线段成比例定理得出AH2=HC2,故AH=HC,从而S△BHA=S△BHC= ![]() S△ABC,得出结论BH不是△ABC的黄金分割线.
S△ABC,得出结论BH不是△ABC的黄金分割线.
【考点精析】通过灵活运用三角形的面积和平行线分线段成比例,掌握三角形的面积=1/2×底×高;三条平行线截两条直线,所得的对应线段成比例即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一位旅行者在早晨8时从城市出发到郊外所走路程与时间的变化图.根据图回答问题:
(1)9时,10时30分,12时所走的路程分别是多少千米?
(2)他中途休息了多长时间?
(3)他从休息后直达目的地这段时间的速度是多少?(列式计算)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(6x4﹣4x3+2x2)÷(﹣2x2)+3x2
(2)(x﹣5)(2x+5)+2x(3﹣x)
(3)(﹣1)2016+(﹣![]() )﹣2﹣(3.14﹣π)0
)﹣2﹣(3.14﹣π)0
(4)运用乘法公式计算:1122﹣113×111
查看答案和解析>>
科目:初中数学 来源: 题型:
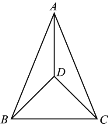
【题目】如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b与反比例函数y= ![]() (x>0)的图象交于A(1,6),B(a,3)两点.
(x>0)的图象交于A(1,6),B(a,3)两点.
(1)求k1和k2的值;
(2)结合图象直接写出k1x+b﹣ ![]() >0的x的取值范围.
>0的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,数轴上的点A、B分别表示数a、b,则点A、B(点B在点A的右侧)之间的距离表示为AB=b﹣a,若点C对应的数为c,满足|a+3|+(c﹣9)2=0.
(1)写出AC的值 .
(2)如图②,点D在点C的右侧且距离m(m>0)个单位,点B在线段AC上,满足AB+AC=BD,求AB的值(用含有m的代数式表示).
(3)如图③,若点D在点C的右侧6个单位处,点P从点A出发以2个单位/秒的速度向右运动,同时点M从点C出发以1个单位/秒的速度也向右运动,当到达D点后以原来的速度向相反的方向运动.求经过多长时间,点P和点M之间的距离是2个单位?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com