[题目]计算(1)(6x4﹣4x3+2x2)÷(﹣2x2)+3x2(2)(x﹣5)+2x(3﹣x)(3)(﹣1)2016+(﹣)﹣2﹣(3.14﹣π)0(4)运用乘法公式计算:1122﹣113×111 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】计算

(1)(6x4﹣4x3+2x2)÷(﹣2x2)+3x2

(2)(x﹣5)(2x+5)+2x(3﹣x)

(3)(﹣1)2016+(﹣)﹣2﹣(3.14﹣π)0

(4)运用乘法公式计算：1122﹣113×111

【答案】(1)2x﹣1；(2)x﹣25；(3)4；(4)1.

【解析】

（1）根据多项式除以单项式和合并同类项可以解答即可；

（2）根据多项式乘多项式、单项式乘多项式可以解答即可；

（3）根据幂的乘方、负整数指数幂、零指数幂可以解答即可；

（4）根据平方差公式可以解答即可．

解：(1)(6x4﹣4x3+2x2)÷(﹣2x2)+3x2

＝﹣3x2+2x﹣1+3x2

＝2x﹣1；

(2)(x﹣5)(2x+5)+2x(3﹣x)

＝2x2﹣5x﹣25+6x﹣2x2

＝x﹣25；

(3)(﹣1)2016+(﹣)﹣2﹣(3.14﹣π)0

＝1+4﹣1

＝4；

(4)1122﹣113×111

＝1122﹣(112+1)×(112﹣1)

＝1122﹣1122+1

＝1．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】完成下列证明过程．

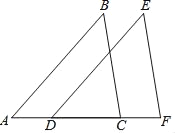
如图，已知AB∥DE，AB＝DE，D，C在AF上，且AD＝CF，求证：△ABC≌△DEF．

证明：∵AB∥DE

∴∠_____＝∠_____（_______）

∵AD＝CF

∴AD+DC＝CF+DC即_____

在△ABC和△DEF中AB＝DE_____

∴△ABC≌△DEF_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中错误的是（）

A.a＜0
B.b＜0
C.c＞0
D.图象过点（3，0）

查看答案和解析>>

科目：初中数学 来源： 题型：

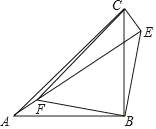
【题目】如图，点E是等腰三角形纸片ABC外一点，∠ABC＝90°，连接AE，点F是线段AE(不与点A，E重合)上一点，在△EBF中，EB＝FB，∠EBF＝90°，连接CE，CF

(1)求证：△ABF≌△CBE；

(2)判断△CEF的形状，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°．朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°，已知A点的高度AB为2米，台阶AC的坡度为1：（即AB：BC=1：），且B，C，E三点在同一条直线上，请根据以上条件求出树DE的高度．（测量器的高度忽略不计）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图甲，点C将线段AB分成两部分（AC＞BC），如果 = ，那么称点C为线段AB的黄金分割点．某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积分别为S1 ， S2（S1＞S2）的两部分，如果 = ，那么称直线l为该图形的黄金分割线．

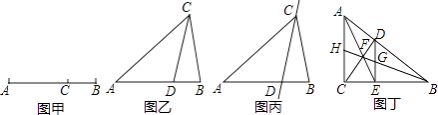
（1）如图乙，在△ABC中，∠A=36°，AB=AC，∠ACB的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；
（2）若△ABC在（1）的条件下，如图丙，请问直线CD是不是△ABC的黄金分割线，并证明你的结论；
（3）如图丁，在Rt△ABC中，∠ACB=90°，D为斜边AB上的一点，（不与A，B重合）过D作DE⊥BC于点E，连接AE，CD相交于点F，连接BF并延长，与DE，AC分别交于点G，H．请问直线BH是直角三角形ABC的黄金分割线吗？并说明理由．