
【题目】如图,直线y=k1x+b与反比例函数y= ![]() (x>0)的图象交于A(1,6),B(a,3)两点.
(x>0)的图象交于A(1,6),B(a,3)两点.
(1)求k1和k2的值;
(2)结合图象直接写出k1x+b﹣ ![]() >0的x的取值范围.
>0的x的取值范围.
【答案】
(1)解:∵直线y=k1x+b与反比例函数y= ![]() (x>0)的图象交于A(1,6),B(a,3)两点,
(x>0)的图象交于A(1,6),B(a,3)两点,
∴k2=1×6=6,3a=6,即a=2,
∴B点坐标为(2,3),
∵一次函数y=k1x+b的图象过A(1,6),B(2,3)两点,
∴ ![]() ,
,
解得 ![]() ,
,
∴k1=﹣3,k2=6;
(2)解:k1x+b﹣ ![]() >0的x的取值范围为1<x<2
>0的x的取值范围为1<x<2
【解析】(1)利用待定系数法求出反比例函数的解析式,然后求出点B的坐标,最后用待定系数法求出直线的解析式;
(2)利用图像直接写不等式的解集,关键弄清楚谁大谁小,谁大就看谁的图像在上方的自变量的取值范围。
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
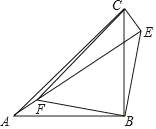
【题目】如图,点E是等腰三角形纸片ABC外一点,∠ABC=90°,连接AE,点F是线段AE(不与点A,E重合)上一点,在△EBF中,EB=FB,∠EBF=90°,连接CE,CF
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图甲,点C将线段AB分成两部分(AC>BC),如果 ![]() =
= ![]() ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果
,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果 ![]() =
= ![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.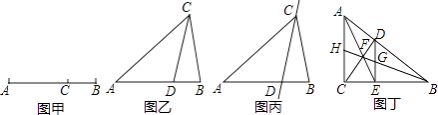
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在公式(a+1)2=a2+2a+1中,当a分别取1,2,3,4,…,n时,可得以下等式:
(1+1)2=12+2×1+1;
(2+1)2=22+2×2+1;
(3+1)2=32+2×3+1;
(4+1)2=42+2×4+1;
……
(n+1)2=n2+2n+1.
将这几个等式的左右两边分别相加,可以推导出求和公式:1+2+3+4+…+n=![]() .
.
请写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有2个完全相同的小球,分别标有数字﹣1,﹣2.现从甲袋中随机抽取一个小球,将标有的数字记录为x,再从乙袋中随机抽取一个小球,将标有的数字记录为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在二次函数y=x2﹣2x﹣2的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BC于C,CD⊥AB于D,点E在AC上,EF⊥AB于F,且∠1=∠2.
(1)试判断CD与EF是否平行并说明理由.
(2)试判断DG与BC是否垂直并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.若AB=8,AD=6 ![]() ,AF=4
,AF=4 ![]() ,则AE的长为 .
,则AE的长为 . 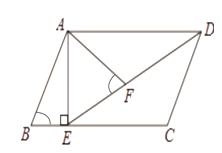
查看答案和解析>>
科目:初中数学 来源: 题型:
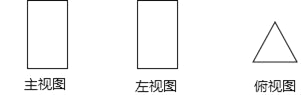
【题目】已知如图为一几何体的三视图:主视图和左视图都是长方形,俯视图是等边三角形
(1)写出这个几何体的名称;
(2)若主视图的高为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com